Nigel Pennick
GEOMETRIA SAGRADA
SIMBOLISMO E
INTENÇÃO NAS ESTRUTURAS RELIGIOSAS
Tradução de ALBERTO FELTRE
EDITORA PENSAMENTO
São Paulo
1980
Índice
Introdução
1. Os Princípios da Geometria Sagrada
2. As Formas
3. A Geometria Britânica Antiga
4. A Geometria Sagrada Egípcia Antiga
5. A Geometria Sagrada Mesopotâmica e Hebraica
6. Grécia Antiga
7. Vitrúvio.
8. Os Comacinos e a Geometria Sagrada Medieval
9. Simbolismo Maçônico e Prova Documental
10. Problemas, Conflitos e Divulgação dos Mistérios
11. A Geometria Sagrada da Renascença
12. A Geometria do Barroco
13. A Geometria Sagrada no Exílio
14. Ciência: O Verificador da Geometria Sagrada
A Albertus Argentinus, inventor do ad quadratum.
"Cada molécula de todo
o universo traz gravada sobre ela a impressão de um sistema métrico, como o
fazem nitidamente o metro dos Arquivos de Paris ou o côvado real duplo do
Templo de Kamak.”
Sir William Herschel.
Gostaria de agradecer às seguintes pessoas por sua variada
colaboração: Major Bernard HaswelI, de Westward Hol; Prudence Jones, de
Cambridge; Martyn Everett, de Saffron Walden, e Michael Behrend, de Epsom.
Introdução
"O homem é a medida de
todas as coisas, dos seres vivos que existem e das não-entidades que não
existem.“
Protágoras (c. 481.411 a.C.)
A geometria existe por toda parte na natureza: a sua ordem
subjaz à estrutura de todas as coisas, das moléculas às galáxias, do menor
vírus à maior baleia. Apesar do nosso distanciamento do mundo natural, nós, os
seres humanos, ainda estamos amarrados às leis. naturais do universo. Os artefatos
singulares planejados conscientemente pela humanidade também têm sido baseados,
desde os tempos mais antigos, em sistema de geometria. Esses sistemas, embora
derivem inicialmente de formas naturais, freqüentemente as ultrapassaram em
complexidade e engenhosidade e foram dotados de poderes mágicos e de profundo
significado psicológico.
A geometria - termo que significa "a medição da
terra" talvez tenha sido uma das primeiras manifestações da
civilização em seu nasce douro. Instrumento fundamental que subjaz a tudo o que
é feito pelas mãos humanas, a geometria desenvolveu-se de uma habilidade
primitiva - a manipulação da medida, que nos tempos antigos era considerada um
ramo da magia. Naquele período antigo, a magia, a ciência e a religião eram de
fato inseparáveis, faziam parte do conjunto de habilidades possuídas pelo
sacerdócio. As religiões mais remotas da humanidade estavam concentradas
naqueles lugares naturais em que a qualidade numinosa da terra podia ser plais
prontamente sentida: entre árvores, rochas, fontes, em cavernas e lugares
elevados. A função do sacerdócio que se desenvolveu ao redor desses sítios de
santidade natural foi a princípio interpretativa. Os sacerdotes e as
sacerdotisas eram os especialistas que podiam ler o significado em augúrios e
oráculos, tempestades, ventos, terremotos e outras manifestações das energias
do universo. As artes do xamanismo que os sacerdotes mais antigos praticavam
permitiram, com uma sofisticação cada vez maior, um sacerdócio ritual
estabelecido que exigiu símbolos externos de fé. Os penedos não desbastados e
as árvores isoladas não mais se constituíam nos únicos requisitos para um local
de adoração. Construíram-se compartimentos, que foram demarcados como lugares
santos especiais separados do mundo profano. No ritual exigido pelo novo plano,
a geometria tornou-se inseparavelmente ligada à atividade religiosa.
A harmonia inerente à geometria foi logo reconhecida como a
expressão mais convincente de um plano divino que subjaz ao mundo, um padrão
metafísico que determina o padrão físico. Esta realidade interior, que
transcende a forma exterior, continuou a ser ao longo de toda a história a base
das estruturas sagradas. Por essa razão é tão válido construir hoje um edifício
moderno de acordo com os princípios da geometria sagrada quanto o era no
passado em estilos tais como o egípcio, o clássico, o românico, o islâmico, o
gótico, o renascentista ou o Art Nouveau. A proporção e a harmonia seguem
naturalmente o exercício da geometria sagrada, que parece correta porque ela é
correta, ligada como está metafisicamente à estrutura esotérica da
matéria.
A geometria sagrada está inextricavelmente ligada a vários
princípios místicos. Talvez o mais importante deles seja aquele que se atribui
ao fundador da alquimia, Hermes Trismegisto, o Três Vezes Grande Heimes.
Esta máxima é o fundamental. "Acima, como abaixo" ou "O que
está no mundo menor (microcosmo) reflete o que está no mundo maior ou universo
(macrocosmo)". Essa teoria da correspondência subjaz a toda a astrologia e
também a grande parte da alquimia, da geomancia e da magia, no sentido de que a
forma da criação universal está refletida no corpo e na constituição do homem.
O homem, por sua vez, na concepção hebraica, foi criado à imagem de Deus -
o templo que o Criador estabeleceu para hospedar o espírito que eleva o homem
para cima do reino animal.
Assim, a geometria sagrada diz respeito não só às.
proporções das figuras geométricas obtidas segundo a maneira clássica com
o uso da régua e compassos, mas também às relações harmônicas das partes de um
ser humano com um outro; à estrutura das plantas e dos animais; às formas dos
cristais e dos objetos naturais - a tudo aquilo que for manifestações do
continuum universal.
1. Os Princípios da
Geometria Sagrada
Os princípios que norteiam disciplinas tais como a geomancia,
a geometria sagrada, a magia ou a eletrônica estão fundamentalmente ligados à
natureza do universo. Dogmas variáveis de diferentes religiões ou mesmo de
grupos políticos podem ditar variações de forma externa, mas os fundamentos
operatórios permanecem constantes. Pode-se fazer uma analogia com a
eletricidade. Para que uma lâmpada elétrica se ilumine é preciso que várias
condições sejam preenchidas. Uma determinada corrente deve alimentar a lâmpada
por meio de condutores isolados com um circuito completo, etc. Essas condições
não são negociáveis. Se algo não estiver correto, a lâmpada não se
acenderá. Os técnicos de todo o mundo devem conhecer os princípios
fundamentais, caso contrário falharão. Esses princípios transcendem as
considerações políticas ou sectárias. Executado acertadamente, o circuito
funcionará igualmente bem num estado comunista, sob uma ditadura militar ou num
país democrático - até mesmo em outro planeta.
Da mesma maneira, os princípios norteadores da geometria sagrada
transcendem as considerações religiosas sectárias. Como uma tecnologia que tem
o objetivo de reintegrar a humanidade no todo cósmico, ela funcionará,
como a eletricidade, para todas as pessoas que observarem os critérios,
não importa quais sejam os seus princípios ou propósitos. A aplicação
universal dos princípios idênticos da geometria sagrada em lugares separados no
tempo, no espaço e por crençàs diferentes atesta a sua natureza transcendental.
Assim, a geometria sagrada foi aplicada nos templos pagãos do Sol, nos relicários
de Ísis, nos tabernáculos de Jeová, nos santuários de Marduk, nos santuários
erigidos em honra dos santos cristãos, nas mesquitas islâmicas e nos mausoléus
reais e sagrados. Em todos os casos, uma cadeia de princípios imutáveis conecta
essas estruturas sagradas.
A geometria é geralmente incluída na disciplina da
matemática; todavia, a matemática numérica, na verdade, derivou da
geometria, que possui uma ordem muito mais fundamental do que a mera manipulação
de números, que é criação do homem.
Nos nossos dias, as razões geométricas são invariavelmente expressas
em termos matemáticos e parece impensável que a geometria pudesse ser separada
da matemática. Todavia, a expressão matemática de razões tais como o pi e a
seção dourada é apenas uma convenção engendrada para uma civilização letrada
adestrada em figuras e em cálculo. Dizendo respeito em primeiro lugar às razões
e às relações, a expressão da geometria em termos de números pertence a um
período posterior do seu desenvolvimento. A complexa geometria do Egito
antigo, que habilitou arquitetos e geômetras a medir o tamanho exato do país,
estabelecer indicadores geodésicos e erigir vastas estruturas como as
pirâmides, era uma arte prática que implicava no seu relacionamento com o
número. Os geômetras gregos, cujo conhecimento eles próprios admitiam provir
dos egípcios, continuaram no nível prático e não se aventuraram nos reinos da
matemática complexa que só existe para provar aquilo que já se conhece. De
fato, foi só no século XVII, com a ascensão do culto particularmente europeu
protestante à ciência, que o cálculo preciso dos números irracionais tornou-se
uma preocupação urgente.
A interpretação da geometria em termos de relações numéricas
é uma racionalização intelectual posterior de um sistema natural para a divisão
do espaço. Tal interpretação surgiu com o divórcio entre a geometria e o corpus
de ciência, magia e metafísica que agora se conhece peto nome de religião
antiga. Muitas razões de comprimento, como por exemplo as raízes quadradas da
maioria dos números inteiros, não podem ser expressas em termos de números
inteiros e; assim, só podem ser apropriadamente descritas em termos geométricos.
Da mesma maneira, a divisão do círculo em 360 unidades conhecidas como graus no
sistema babilônico convencional não é absoluta. Embora seja geometricamente
derivada, é apenas uma questão de conveniência.
O número, todavia, tal como expresso nas dimensões sagradas
dos edifícios santificados, tem sido freqüentemente usado para camuflar a sua
geometria sagrada subjacente. O Tabernáculo Hebraico e o Templo âescrito na
Bíblia, e também as dimensões da Capela do King's College, em Cambridge, são
tidos como medições que podem ser interpretadas pelos cognoscenti em termos de
geometria mística. O rei Henrique VI só poderia conceber a forma da sua
Capela em Cambridge em termos de medidas que não divulgassem os mistérios
maçônicos aos não-iniciados. Reginald Ely, seu mestre maçom, teve de desenhar
as dimensões como um plano que determinasse a geometria ad triangulum inerente
àquelas dimensões. Por ser a geometria uma imagem da estrutura do cosmos,
ela pode ser facilmente utilizada como um sistema simbólico para a compreensão
de várias estruturas do universo. Essa função simbólica é exemplificada por um
instrumento científico pouco conhecido que foi usado nos tempos pré-coloniais
para ensinar aos meninos polinésios os fundamentos da navegação. Embora os
polinésios não tenham possuído nenhum dos instrumentos agora tidos como
necessários à navegação - o sextante, o compasso e o cronômetro -, eles eram
capazes de viajar regularmente através de grandes extensões do oceano e chegar
aos seus objetivos. Valendo-se das estrelas e de outras características físicas
- como a presença de bancos de nuvem sobre a terra -, os navegadores polinésios
podiam detectar a presença de ilhas, mas o método mais útil era a leitura das
ondas. Assim como qualquer outro objeto marítimo, uma rocha por exemplo,
exercerá um efeito sobre o padrão das ondulações, também a presença de uma
ilha, em escala muito maior, causará padrões de difração nas ondas a muitas
milhas de distância.
A ciência do reconhecimento das ondas era ensinada aos
meninos por meio de um sistema mnemônico, o mattang. Em sua forma
característica, esse instrumento, composto de varetas dispostas num padrão
geométrico preciso, apresentava estranham ente algumas das idéias da geometria
sagrada européia. Esse dispositivo geométrico mostrava aos discípulos todos os
padrões básicos que as ondas formam quando são dobradas pela terra. Da mesma
maneira, todos os padrões geométricos refletem, além disso, verdades que estão
muito além das suas simples derivações, mesmo os complexos relacionamentos com
outras geometrias. A estrutura deles está em harmonia com o universo e com
todas as formas físicas, estruturais e psicológicas que constituem a sua
unicidade.
Desde os tempos mais antigos, a geometria foi inseparável da
magia. Mesmo os riscadores-de pedra mais arcaicos têm forma geométrica. Eles
apontam para um sistema notacional e invocacional praticado por algum antigo
sacerdócio. Pelo fato de as complexidades e as verdades abstratas expressas
pela forma geométrica só poderem ser explicadas como reflexos das verdades mais
íntimas da substância do mundo, elas eram consideradas como mistérios sagrados
da ordem mais elevada e eram ocultadas dos olhos profanos. Um conhecimento
especial era exigido para se desenhar tais figuras e a sua importância mística
era ignorada pelas massas sem instrução. Os conceitos complexos eram
transmitidos de um iniciado a outro por meio de símbolos geométricos
individuais, ou combinações deles, sem que o ignorante nem ao menos suspeitasse
de que estava ocorrendo uma comunicação. Como o sistema moderno de símbolos secretos
empregado pelos ciganos, eles deveriam constituir-se em enigmas
embaraçosos para o curioso.
Toda forma geométrica está investida de significado
psicológico e simbólico. Assim, tudo aquilo que é feito pelas mãos do homem e
que incorpora esses símbolos de uma maneira ou de outra torna-se um veículo
para as idéias e as concepções corporificadas em sua geometria. Através
dos tempos, as geometrias simbólicas complexas agiram como a base para a arquitetura
sagrada e profana, variando a geometria de acordo com a função. Algumas
geometrias continuam sendo ainda hoje poderosas imagens arquetípicas da fé:
logo acorre à nossa mente, com símbolo do judaísmo, o hexagrama. Outras geometrias
foram menos conhecidas pelo público, sendo usadas para indicar àqueles que
"estavam a par" alguma verdade esotérica, como o vesica piscis do
tampo da Fonte Chalice em Glastonbury. Outras, todavia, estão ocultas nas
profundezas dos artefatos místicos - ou até mesmo nas brincadeiras das
crianças.
Uma brincadeira bastante comum entre escolares é uma reminiscência
de um antigo sistema de geometria sagrada. Conhecido como "ler a
sorte", o jogo envolve a dobradura de um quadrado de papel de uma
determinada maneira. De qualquer jeito que o abrirmos, sempre se nos revelará
uma de quatro opções. A dobradura do papel e a forma que ele toma quando
desdobrado são um dispositivo mnemônico para a criação da geometria ad
quadratum usada pelos antigos maçons.
Toma-se um quadrado de papel e dobram-se os quatro
cantos de maneira que eles se encontrem. Este procedimento produz um novo
quadrado, cuja área corresponde à metade do quadrado original. Estes cantos -
são novamente dobrados de dentro para fora, o que cria um outro quadrado
correspondente à metade do anterior e produz uma divisão óctupla. Pode-se
fazer, a partir daí, uma figura tridimensional, com dois grupos de
"vértices" que podem ser abertos e fechados à vontade. A associação
dessa geometria muito bem definida com a leitura da sorte pode ser
perfeitamente o resíduo deteriorado de um antigo sistema de adivinhação, pois o
padrão assim formado não só reproduz a configuração básica do ad quadratum, mas
também o esboço tradicional do desenho do horóscopo. Este último padrão combina
de maneira engenhosa a divisão óctupla pagã do quadrado com a divisão
duodécupla oriental do zodíaco.
O uso de formas geométricas é bastante conhecido na magia
ritual, tanto para a evocação de espíritos e poderes quanto para a proteção do
mágico contra suas cortesias malévolas. Cada espírito tem tradicionalmente
um sigilo ou padrão geométrico associado ao seu nome, por meio do qual, com
conjuras e rituais apropriados, ele pode ser contactado. Muitos desses sigilos
são expressões geométricas dos nomes e são produzidos pelo traçado de números
equivalentes às letras sobre. quadrados mágicos. A determinação dos números
equivalentes aos nomes é conhecida como gematria. Nos alfabetos grego e
hebraico, cada um dos caracteres representa não só um som, mas também um
equivalente numérico. Assim, o nome Israel poderia ser escrito em hebraico da
seguinte maneira: Yod Shin Resh Aleph Lamed. Esses caracteres têm o
equivalente numérico 10, 300, 200, 1, 30 = 541. Uma convenção da gematria permite,
assim, que outras palavras de valor numérico equivalente possam ser usadas
como seus substitutos. Os cabalistas, durante muitos séculos, estudaram o
significado oculto do livro de Isaías segundo esses critérios. A
substituição de uma palavra por outra pode ser usada como um método oculto de
comunicação que elimina a necessidade de se usar um nome que tenha poderes
especiais próprios. Também é possível traçar esquemas a partir das posições
ocupadas pelos números nos quadrados mágicos. Assim, o nosso exemplo, Israel,
esquematizado sobre o Quadrado Mágico do Sol, cria um sigilo específico que
pode ser depois transferido para os utensílios mágicos, etc. (ver Figura 4).
Onde quer que a geometria tenha sido usada, consciente ou
inconscientemente, o seu simbolismo ainda se faz presente. Através de todo o
universo conhecido, a função da sua geometria é um valor imutável da existência
transitória. Os artistas e os mágicos reconheceram essa qualidade
transcendental e, em conseqüência, constituíram a base imutável sobre a qual
está apoiado o tecido da cultura. Através de toda a história registrada, o
geômetra trabalhou silenciosamente em sua arte, fornecendo a matriz interna
sobre a qual se baseiam as formas externas.
2. As Formas
São muito poucas as formas geométricas básicas das quais se
compõe toda a diversidade da estrutura do universo. Cada uma delas é dotada de
propriedades únicas e detém um simbolismo esotérico que permaneceu imutável ao
longo da história humana. Todas essas formas geométricas básicas podem ser
facilmente produzidas por meio dos dois instrumentos que os geõmetras têm usado
desde a aurora da história - a régua e o compasso. Figuras universais, sua construção
não exige a utilização de nenhuma medição; ocorrem em todas as formações
naturais, nos reinos orgânico e inorgânico.
O círculo
Talvez o círculo tenha sido o símbolo mais antigo desenhado
pela raça humana. Simples de ser executado, é uma forma cotidiana encontradiça
na natureza, vista nos céus como os discos do sol e da lua, e ocorre nas formas
das plantas e dos animais e nas estruturas geológicas naturais. Nos tempos
antigos, as construções, fossem elas temporárias ou permanentes, eram
circulares em sua grande maioria. Os nativos americanos tipi e os yurt
mongólicos atuais são sobreviventes de uma antiga forma universal. Dos círculos
de cabanas da Grã-Bretanha neolítica, desde, os círculos de pedra megalíticos
até as igrejas e os templos redondos, a forma circular imitou a redondeza do
horizonte visível, fazendo de cada construção, na verdade, um pequeno mundo em
si mesmo.
O círculo representa o completamento e a totalidade, e as
estruturas redondas ecoam peculiarmente esse princípio. No Rosarium
Philosophorum, um antigo tratado aIquímico, lemos a seguinte afirmação:
"Faze um círculo ao
redor do homem e da mulher e desenha fora dele um quadrado e fora do quadrado
um triângulo. Faze um círculo ao redor dele e terás a pedra dos filósofos.”
O círculo contém aí a imagem do homem, como no famoso desenho
virtuoso de Leonardo da Vinci. Com base nesta figura fundamental, pode-se
produzir o quadrado e, depois, as outras figuras geométricas. A pedra dos
filósofos, a súmula de todas as coisas e a chave para o conhecimento, é
produzida dessa maneira e representada pelo círculo, a figura matriz de que
podem ser geradas todas as outras figuras geométricas. Com régua e compasso,
todas as figuras importantes eram produzidas simples e elegantemente. Essas
figuras - o vesica piscis, o triângulo eqüilátero, o quadrado, o hexágono e o
pentágono -, todas elas mantêm relações diretas umas com as outras.
O quadrado
Os templos antigos eram freqüentemente construídos em forma
quadrilátera. Representando o microcosmo e, em conseqüência, considerada como
um emblema da estabilidade do mundo, essa característica era especialmente
verdadeira para as representações artificiais de montanhas que reproduziam o
mundo, para os zigurates, as pirâmides e as estupas. Essas estruturas
simbolizavam o ponto de transição entre o céu e a terra e centralizavam
idealmente o omphalos, o ponto axial do centro do mundo.
Geometricamente, o quadrado é uma figura única. Pode ser
dividido com precisão por dois e por múltiplos de dois apenas com um esboço.
Também pode ser dividido em quatro quadrados quando se faz uma cruz que define
automaticamente o centro exato do quadrado. O quadrado, orientado para os
quatro pontos cardeais (no caso das pirâmides egípcias, com um exatidão fenomenal),
pode ser novamente bisseccionado por diagonais, que o dividem em oito
triângulos. Essas oito linhas, partindo do centro, formam os eixos que indicam
as quatro direções cardeais e os "quatro cantos" do mundo - a divisão
óctupla do espaço.
Essa divisão óctupla do espaço é venerada no "caminho
óctupIo" da religião budista e nas "Quatro Estradas Reais da Grã-Bretanha"
relatadas minuciosamente na History of the Kings of Britain, de Geoffrey of
Monmouth. Cada uma das direções, no Tibete, estava sob a guarda simbólica
hereditária de uma família, tradição que encontrou paralelo na Grã-Bretanha nas
oito Famílias Nobres que sobreviveram à Cristianização e produziram os reis e
os santos da Igreja Celta.
A divisão óctupla do quadrado era; na tradição européia, um
emblema da divisão do dia e do ano, bem como da divisão do país e da sociedade.
Embora a divisão óctupla do tempo fosse gradualmente eliminada com o advento do
sistema duodécuplo dos cristãos, ela sobreviveu nos antigos quarterdays
[primeiro dia de um trimestre] do calendário, nas tradicionais festas do fogo
nos países pagãos e na geometria maçônica da arquitetura sagrada do sistema
acht uhr ou ad quadratum. Voltarei a esse assunto importante num capítulo
posterior.
O hexágono
O hexágono é uma figura geométrica natural produzida pela
divisão da circunferência de um círculo por meio dos seus raios. Os pontos da
circunferência são conectados por linhas retas e produzem uma figura com seis
lados iguais.
Sendo uma função da relação entre o raio e a circunferência
do círculo, o hexágono é uma figura natural que ocorre em toda a natureza. É
produzido naturalmente na fervura e na mistura de líquidos. O físico francês
Bénard observou, durante as suas experiências de difusão em líquidos, que os
padrões hexagonais se formavam freqüentemente em toda a superfície. Tais
tourbillons cellulaires, ou "células de Bénard", foram objeto de
muitos experimentos. Verificou-se que, em condições de perfeito equilíbrio, os
padrões formavam hexágonos perfeitos. Esses padrões eram semelhantes aos das
células que constituem a vida orgânica ou as formas prismáticas das rochas
basálticas. Sujeitos às mesmas forças universais de viscosidade e de difusão,
padrões similares são criados naturalmente num líquido fervente.
O hexágono natural mais bem conhecido é aquele que se vê nos
favos das abelhas. Esses favos são formados de uma reunião de prismas hexagonais
cuja precisão é tão espantosa, que atraiu a atenção de muitos filósofos, que
viam neles uma manifestação da harmonia divina na natureza. Na Antigüidade,
Pappus, o Alexandrino, dedicou a sua atenção a esse esquema hexagonal e chegou
àconclusão de que as abelhas eram dotadas de uma "certa intuição
geométrica", com a economia como princípio orientador, pois, "existindo
três figuras que podem ocupar o espaço que circunda um ponto - a saber, o
triângulo, o quadrado e o hexágono -, as abelhas escolheram sabiamente como sua
estrutura aquela que possui mais ângulos, suspeitando com certeza que ela
poderia conter mais mel do que qualquer uma das outras duas".
Em minhas próprias pesquisas sobre a estrutura dos microrganismos
marinhos, encontrei o hexágono na forma externa da Pyramimonas virginica, uma
alga marinha norte-americana. Nela, as bases das estruturas que cobrem o corpo
do organismo formam hexágonos perfeitos, embora elas sejam menores que o
comprimento da onda da luz visível. Essa geometria natural sobre a qual o autor
romano Plínio nos conta que os homens fizeram do seu estudo o trabalho de toda
uma vida em sua época, é de interesse especial para o geômetra místico.
A relação direta do hexágono com o círculo está ligada a uma
outra propriedade interessante segundo a qual os vértices alternados dessa
figura podem ser conectados por linhas retas para a produção do hexagrama. Essa
figura, composta de triângulos eqüiláteros que se interpenetram, simboliza a
fusão dos princípios opostos masculino e feminino, quente e frio, água e fogo,
terra e ar, etc. e é, por conseguinte, símbolo da inteireza arquetípica, o
poder divino da criação. Assim, foi usada na alquimia e continua sendo o
símbolo sagrado dos judeus ainda em nossos dias. As dimensões dos triângulos
que formam o hexagrama estão diretamente relacionadas ao círculo que as produz
e podem ser o ponto de partida para desenvolvimentos geométricos.
O vesica piscis, o triângulo
e os sólidos platônicos
O vesica piscis é aquela figura que se produz quando dois círculos
de igual tamanho são desenhados, um a partir do centro do outro. Em termos
geométricos sagrados, trata-se do ponto de derivação do triângulo eqüilátero e
da linha reta que parte do círculo. Representou os órgãos genitais da Deusa
Mãe, o ponto físico de origem da vida simbolizada por sua posição fundamental
na geometria. Por essa razão, ocupou uma posição privilegiada na construção
de edifícios sagrados. Dos círculos de pedra e dos templos mais antigos até as
catedrais do período medieval, o ato inicial da construção foi relacionado ao
nascer-do-sol de um dia predeterminado. Esse nascimento simbólico do templo
com o novo sol é um tema universal e sua conexão com o vesica de forma genital
não é mero acidente. A geometria do templo hindu, como as das suas contrapartidas
espirituais da Ásia Menor, da África Setentrional ou da Europa, está registrada
como sendo diretamente derivada da sombra de um poste ou gnomon. O Manasara
Shilpa Shastra, um antigo texto sânscrito sobre construção de templos, detalha
a derivação do plano a partir da orientação.
Escolhido o sítio por um praticante de geomancia, um poste
era cravado no chão naquele local. Um círculo era desenhado ao seu redor. Esse
procedimento produz um eixo leste-oeste verdadeiro. De cada ponta desse eixo,
desenhavam-se arcos, produzindo-se então um vesica piscis que, por sua vez,
fornecia um eixo norte-sul. Assim, o vesica universal era fundamental para a
construção do templo. Com base nesse vesica inicial, desenhava-se um outro a
partir do ângulo reto e, com base nele, um círculo central e depois um quadrado
dirigido para os quatro quartos da terra.
O sistema hindu de construção pode ser considerado fundamentalmente
idêntico ao utilizado no método romano de construção de cidades e descrito nas obras
de Vitrúvio. É produzido por observação direta e, assim, reproduz as condições
predominantes no momento exato da fundação. Essa fixação no tempo, como o
momento do nascimento na astrologia, é fundamental em todas as práticas
de orientação, exatamente como um alinhamento incorporaria automaticamente
os atributos astronômicos e astrológicos do tempo. Além disso, as
características geomânticas do local, que lhe conferem uma feição única, são
incorporadas ao templo.
O vesica não está envolvido na construção por princípios arbitrários.
Ele é o ponto prático de partida do qual derivam todas as outras figuras
geométricas. Dividindo-se o vesica com uma linha que passa pelos centros
dos dois círculos, unindo-se os seus vértices comuns e, para um lado e para o
outro, ligando-se esses vértices aos pontos em que a linha vertical cruza os
círculos, obtêm-se dois triângulos eqüiláteros. Os lados desses triângulos são
de comprimento igual ao raio do círculo gerador. Com base no triângulo eqüilátero,
pode-se produzir facilmente o hexágono e o icosaedro. Em termos esotéricos,
toda a série de sólidos geométricos regulares conhecida universalmente como
Sólidos Platônicos pode ser produzida a partir de figuras planas.
No Timeu, Platão escreveu: "Ora, a figura [triângulo]
que tenho dito ser a mais bela de todos os muitos triângulos (não é ne o
cessário falar dos outros) é aquela cujo duplo forma um terceiro triângulo que
é eqüilátero (...) escolhamos então dois triângulos, com que foram construídos
o fogo e outros elementos, um isósceles, tendo o outro o quadrado do lado maior
igual a três vezes o quadrado do lado menor".
No sistema de Pia tão, o simbolismo geométrico encarrega-se
de registrar todos os estados conhecidos da matéria. Especialmente importante
era a série de figuras sólidas que era a essência da sua filosofia. Por meios
ocultos, toda a série era simbolizada numa figura agora ostentada pelos
franco-maçons do grau do Santo Arco Real. Esse símbolo é o triângulo eqüilátero
circunscrito num hexagrama. "Analisa"-se seu simbolismo somando-se os
valores dos ângulos produzidos pelas várias partes e dividindo-se por tantos
ângulos retos que tiverem igual valor. Esse método arcano possibilita que
qualquer figura geométrica seja "analisada" e, assim, impregna a sua simplicidade
com um rico simbolismo que foi explorado a fundo pelos arquitetos de
construções sagradas.
O triângulo eqüilátero determinado dentro do tetraedro é
igual em valor geométrico aos oito ângulos retos - o número de graus em quatro
triângulos eqüiláteros. Em virtude de ser o menor sólido geométrico
regular e por causa da sua forma piramidal, foi utilizado pelos platônicos para
representar o elemento fogo.
Os triângulos "determinados" no hexagrama ou Sigilo
de Salomão, sem levar em consideração as intersecções (que convencionalmente
são mais entrelaçamentos do que junções), são equivalentes a dezesseis ângulos
retos. Este é o número contido no octaedro, o sólido platônico composto de oito
triângulos eqüiláteros de lados iguais. Ele foi atribuído pelos platônicos ao
elemento ar, o mais próximo do tetraedro em leveza.
Ignorando-se as intersecções, à Sigilo de Salomão, com seu
triângulo menor superposto, se igualará ao número de graus dos 24 ângulos. Este
é o número que está no cubo, um sólido composto de seis quadrados iguais. Essa
figura sólida e fixa simbolizava para os platônicos o elemento terra. Ele
representou universalmente esse elemento onde quer que ele ocorresse na
geometria sagrada - a base quadrangular do templo e da Cidade Sagrada, plantada
fixamente sobre o omphalos.
O triângulo invertido do sigilo, com o triângulo menor
circunscrito, somado ao triângulo maior do hexagrama voltado para cima, perfaz
quarenta ângulos retos, iguais em graus àqueles que estão no icosaedro, um
regular formado por vinte triângulos eqüiláteros de lados iguais. Este é o
sólido regular mais pesado formado por triângulos. Próximo ao cubo em peso, o
icosaedro representou o elemento água. Assim, considera-se que toda forma que
derivou do hexagrama, com seu triângulo interno, incorpora todos os sólidos
platônicos e, por associação, os quatro elementos - um atributo da
universalidade e um símbolo da lei da unidade dos opostos.
A Seção Dourada
A Seção Dourada é uma razão que foi usada na artesania sofisticada
e na arquitetura sagrada do Egito antigo. No antigo Egito e na Grécia, ocorreu
um uso extensivo daquilo que Jay Hambidge, geômetra do início do século XX,
chamou de "simetria dinâmica". Os objetos e os edifícios sagrados
egípcios e gregos possuem geometrias baseadas na divisão do espaço conseguida
pelos retângulos de raiz e seus derivados. Os retângulos de raiz são produzidos
diretamente do quadrado por simples desenho com um compasso e, assim, fazem
parte da geometria clássica, produzida sem medição.
Existe toda uma série de retângulos de raiz. O primeiro dos
retângulos de raiz é o quadrado, que é um retângulo "de raiz 1". O
seguinte, o retângulo V2, é produzido a partir do quadrado por meio do simples
expediente de se colocar o compasso no comprimento da diagonal e fazer a linha
de base encontrar a linha traçada a partir daquele vértice. Esse procedimento
torna o comprimento do lado longo igual à raiz quadrada de 2, tomando-se o lado
curto como unidade. O retângulo V3 é produzido a partir da diagonal desse
retângulo, e assim por diante.
Embora os lados desses retângulos não sejam medidos em termos
de número, os gregos diziam que essas linhas não eram irracionais porque eram
mensuráveis em termos dos quadrados produzidos por elas. A mensurabilidade em
termos da área do quadrado, em vez do comprimento, era o grande segredo da
antiga geometria sagrada grega. O famoso teorema de Pitágoras, conhecido de
todo escolar, só é compreensível em termos da medida do quadrado. Por exemplo,
a relação entre o final e o lado de um retângulo V5 é uma relação de área
porque o quadrado construído ao final de um retângulo V5 é exatamente um quinto
da área de um quadrado construído sobre seu lado. Tais retângulos possuem a
propriedade de serem divididos em formas muito menores que também são partes
mensuráveis do todo.
Isto nos leva a um outro fator fundamental no desenho da
arquitetura sagrada: a proporção e a sua irmã siamesa, a comensurabilidade. A
música o demonstra admiravelmente em suas harmonias e, com efeito, já se disse
que a música é na realidade a geometria traduzida em som, pois na música
pode-se ouvir as mesmas harmonias que sustentam a proporção arquitetônica. A
comensurabilidade, que garante harmonia completa em toda a construção ou obra
de arte, é uma integração racional de todas as proporções de todas as partes de
uma construção de maneira que toda parte tenha forma e tamanho absolutamente
fixos. Nada pode ser acrescentado ou removido desse conjunto harmonioso sem
romper a harmonia do todo. Certos retângulos, que são o ponto de partida para
figuras geométricas relacionadas, geralmente constituem as bases de tais padrões
harmonizadores.
Retângulos que possuem as razões lado: lado iguais a 3:2,
5:4, 13:6, etc., em que as proporções são expressas em números inteiros, têm
recebido o nome de retângulos estáticos. Retângulos do tipo dos retângulos de
raiz têm sido chamados de retângulos dinâmicos. Esses últimos são mais
encontradiços na composição geométrica. Eles permitem uma flexibilidade muito
maior de uso do que os retângulos estáticos, especialmente quando são usados
para se estabelecer a harmonia dos elementos pela proporção.
Há alguns retângulos que combinam as características dos
retângulos estáticos e dinâmicos. São o quadrado e o quadrado duplo (1 = 1:1 =
V1:1 e 2 = 2:1 = V4:1). A diagonal do quadrado duplo, que talvez seja a forma
mais favorecida pelos edifícios sagrados, é V5. Esse número irracional
relaciona diretamente o retângulo de raiz 2 ou de raiz 4 ao retângulo de raiz
5, que está diretamente relacionado a proporção V5 + 1 da seção dourada.
2
Essa importante razão, chamada de Seção pelos gregos antigos,
de Proporção Divina por Luca Pacioli (1509) e de Seção Dourada por Leonardo e
seus seguidores, tem propriedades únicas que a recomendaram aos geômetras desde
os tempos egípcios.
A Seção Dourada existe entre duas quantidades mensuráveis de
qualquer espécie quando a razão entre a maior e a menor é igual à razão entre a
soma das duas e a maior delas. Em termos geométricos, ela pode ser facilmente
produzida a partir do quadrado duplo. Se um dos dois quadrados for cortado ao
meio e a diagonal dessa metade for levada para baixo em direção à base, o lugar
em que ela corta a base representará 1,618 unidades em relação ao lado do quadrado
que tem unidade 1 de comprimento. A razão também pode ser produzida a partir do
pentagrama e está associada ao pentágono, quando então a razão entre o
lado do pentágono e a sua extensão para o pentagrama obedece à
equação V5 + 1 = 1,618...
2
Na convenção geométrica grega, isto está simbolizado pela
letra grega (I). Numericamente, possui propriedades algébricas, matemáticas e
geométricas excepcionais. (I) = 1,618; (I) = 0,618 e (I) 2 = 2,618.
Em toda progressão ou série crescente de termos que tem como
a razão entre os termos que se sucedem, cada termo é igual à soma dos dois
precedentes. Esta propriedade singular permite a manipu lação de toda a
série. Todos os outros termos sucessivos podem ser construídos, a partir
de dois deles, por movimentos simples do compasso.
Em termos numéricos, essa série aditiva foi popularizada peja
primeira vez na Europa por Leonardo Bigollo Fibonacci, conhecido como Leonardo
da Pisa. Nascido em 1179, Leonardo viajou com seu pai para Algiers, onde
aprendeu, com os geômetras árabes, o segredo da série e por essa razão pôde
introduzir os números arábicos na Europa. Ambos os conceitos revolucionaram a
matemática européia.
Esta série numérica, conhecida agora pelo nome de Série Fibonacci,
foi há muito tempo reconhecida como um princípio que ocorre na estrutura dos
organismos vivos e, por conseguinte, um princípio inerente à estrutura do
mundo. Sua construção é enganosamente fácil: o termo seguinte é a soma dos
dois termos anteriores, isto é, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, e
assim por diante. O arranjo das folhas de um vegetal, os hipotênares da
pata do gato e as espirais das conchas formainíferas microscópicas são
governados peja Série Fibonacci.
A Seção Dourada tem sido reverenciada através de toda a história.
Platão, em seu Timeu, discutiu-a como a chave da física do Cosmos. Luca
Pacioli, geômetra renascentista, publicou sua influente obra De Divina
Proportione em Veneza em 1509 e até mesmo o arquiteto moderno Le
Corbusier, pai dos grupos de prédios, planejou um sistema modular de
proporção baseado nessa antiga mas poderosa razão.
3. A Geometria Britânica
Antiga
"As estruturas sagradas
e culturais pró-cristãs só podem ser compreendidas se se adotar o ponto de
vista dos antigos. Para eles, todas as coisas mundanas estavam vinculadas às
coisas divinas. Todos os pensamentos e todas as ações humanas estavam
subordinados às influências energizantes das forças divinas onipotentes. Sua
filosofia e sua sabedoria culminaram no conhecimento de que como o acima, assim
também o abaixo e na tentativa de harmonizar todas as suas atividades e
ambições com a natureza superior, a Vontade Divina.”
Josef Heinsch.
Espalhados por todas as Ilhas Britânicas e por toda a Europa
Setentrional estão os últimos remanescentes de uma cultura perdida há muito
tempo: as pedras eretas. Lembranças grosseiras de uma era quase
inimaginavelmente distante, os megalitos da Europa ainda sobrevivem em número
considerável. Apesar de talvez a maior parte deles ter desaparecido nos
3.000-5.000 anos que se passaram desde que foram erigidos, muitos sítios ainda
sobrevivem virtualmente intactos.. Alguns desses megalitos enigmáticos são
solitários e desbastados; outros estão arranjados em formações complexas. Mas
há outros que foram enfeitados e apresentam entalhes tanto figurativos quanto
abstratos.
Alguns dos entalhes mais arcaicos e enigmáticos que foram executados
sobre rochas e que sobrevivem até hoje são os sinais. de cálices e de anéis
que podem ser encontrados nas pedras eretas e, menos comumente, nos
afloramentos naturais de rochas. Durante muitas centenas de anos, esses
entalhes foram fontes de lenda, objeto de veneração para os supersticiosos e
motivo de comentário e de especulação para os antiquários locais. Muitos
comentadores eruditos aventuraram-se em discutir sobre sua função e seu
significado, que ainda continuam a ser um quebra-cabeças a ser resolvido
no campo da pesquisa pré-histórica.
Seus desenhos são variados, repetindo-se raramente,
espalhados sobre a pedra sem qualquer ordem óbvia. Os sinais de cálices e de
anéis consistem de pequenas depressões semelhantes a cálices, geralmente
circulares, mas assumem ocasionalmente uma forma oval. Freqüentemente esses
"cálices" estão cercados por anéis concêntricos. Às vezes são
excêntricos ou aneliformes. Variam em número e podem ser associados a linhas
radicais que atravessam completamente os anéis e às vezes ligam o sistema
cálice-anel a um outro sistema, situado numa parte diferente da superfície da
rocha. As espirais são raras, como também os entalhes que lembram escadas. Na
Irlanda, são comuns os desenhos que semelham estrelas ou sóis redondos com
linhas que delas saem imitando raios. Estes últimos correspondem a alguns dos
hieroglifos dos antigos traços escandinavos executados sobre rochas conhecidos
como hällristningar, que foram os precursores dos caracteres rúnicos. Embora
esses petroglifos se estendam desde a Europa até a Ásia, variações locais são
amiúde suficientes para distinguir as marcas de uma localidade das de outra.
Inúmeras conjecturas foram feitas no sentido de se
compreender o significado dos sinais de cálices e de anéis. Os autores os
classificaram como marcadores territoriais tribais, mapas de aldeias préhistóricas
com suas estradas, "árvores" genealógicas, uma espécie de escrita
indecifrada, canais para o sangue sacrificial, mapas das posições das pedras
eretas ou casas figurativas dos mortos.
Um dos poucos estudos sistemáticos do significado desses
sinais inescrutáveis foi executado pelo antiquário escocês Ludovic MacLeIlan
Mann, um pesquisador independente cuja obra hoje pouco se conhece. Em 1915,
publicou Archaic Sculpturings, em que confrontou os resultados de um grande
número de anos de pesquisa dos entalhes em rocha. Após a análise, MacLellan
Mann chegou à conclusão de que os sinais de cálices e de anéis faziam parte de
um sistema coerente. Ein Archaic Sculpturings, MacLellan Mann escreveu:
"Alguns anos atrás (...) comecei a fazer um exame dos
muitos grupos desses sinais e, para meu espanto, descobri que, em vez de os
sinais terem sido feitos a esmo, eles estavam arranjados da maneira mais precisa,
matemática e geométrica. (...) Embora essas esculturas ofereçam tipos
marcadamente di. ferentes. elas foram executadas em obediência às mesmas idéias
e segundo o mesmo sistema. Observei que as linhas retas podem ser desenhadas em
determinadas partes, tais como ao longo dos conjuntos de canaletas
freqüentemente metódicas ou através dos centros de três ou mais cálices ou
conjuntos aneliformes. Quando executadas, estas linhas tinham de convergir
precisamente para os pontos focais comuns situados além do campo das esculturas.
(...) Ao redor de cada um desses focos deveria estar um conjunto de zonas
concêntricas, muitas das quais conformam as partes principais ou essenciais da
obra esculpida tão exata e tão freqüentemente, a ponto de apontarem para algum
fator que não é o acaso, o acidente ou a coincidência.”
A análise de Mann da geometria subjacente que ele descobriu
nas marcas de cálices e de anéis foi interpretada em termos astronômicos. Há
dois centros principais que determinavam os sinais pelas zonas radiais e
concêntncas geradas a partir deles. Um centro, Mac Lellan Mann acreditava, era
freqfientemente cortado por uma linha que representava uma linha norte-sul
exata, e pelo outro centro passava uma segunda linha norte-sul a quatro graus
numa direção divergente. Assim, dois sistemas complementares de linhas encaixavam-se
nas partes salientes dos talhes. Um relacionava-se ao norte terrestre - o pólo
atual do planeta terra -, ao passo que o outro era determinado pela posição da
estrela polar ou norte magnético. MacLellan Mann acreditava que sua grande
radial, dentro da qual eram feitos os entalhes, era um sistema de referência
que mostrava as posições dos corpos celestes em determinados momentos do ano.
Esses entalhes astronômicos foram encontrados em todo o continente. Datando de
mais de 30.000 anos, foram elaborados por sociedades iletradas, mas não
pré-astronômicas.
Os fatos de astronomia foram lentamente acumulados durante
séculos de observação direta e registro, uma técnica que não envolveu a
utilização da escrita, tal como a conhecemos hoje. Os segredos da astronomia eram
desvendados por ensaio e erro e pelo expediente da observação das estrelas.
Tendo desenvolvido a função de elaboração de calendários, e daí a de registrar
a atividade celestial, os sacerdócios antigos que organizaram tais assuntos
precisavam de algum método para determinar o tempo preciso Ido ano para a
realização de cada uma das suas observâncias práticas e rituais.
A necessidade fundamental de determinar os tempos precisos em
que os ritos mágicos ou religiosos deveriam ser cumpridos é demonstrada nos
dias atuais pelos rituais da tribo norte-americana dos hopi. Em determinadas
épocas do ano, os sacerdotes e os membros das sociedades religiosas descem para
os seus kivas (santuários subterrâneos) e observam as estrelas pela entrada
vertical. Várias canções apropriadas e alguns gestos são executados durante o
tempo em que as constelações importantes passam por sobre a entrada. A duração
de toda a cerimônia é, assim, determinada pela passagem das estrelas.
Dessa maneira, os ritos são harmonizados por observação direta com as
condições- astronômicas e astrológicas predominantes.
Algo similar deve ter sido a motivação daqueles que
construíram os observatórios megalíticos da Europa. A única maneira de fazê-Io
era construir pontos de observação que medissem e definissem precisamente a
passagem do tempo. Essa necessidade levou à descoberta de que os cicIos de
ascensão e de decIínio do sol, da lua e das estrelas não estão sujeitos a leis
simples.
Esse despertar gradual na compreensão reflete-se nos restos
da cultura megalítica da Grã-Bretanha, onde a arqueologia mostrou que os
observatórios de pedra e de madeira foram reconstruídos a intervalos. Cada
reconstrução incorporava incrementos progressivos em complexidade e
sofisticação. A construção de observatórios cada vez mais complexos andava de
mãos dadas com a invenção e o emprego de geometrias também cada vez mais
complexas. Conhecimento considerável e destreza eram exigidos para o desenhó,
o planejamento e a construção de um empreendimento tal como o de Stonehenge.
Encontrar o sítio correto para a observação dos fenômenos celestes e a
colocação ali de enormes pedras eretas que marcavam exatamente a passagem dos
corpos celestiais exigia uma ciência exata da geometria aplicada.
MacLellan Mann descobriu que ela existiu realmente A geometria
subjacente que ele detectou nos sinais de cálices e de anéis também poderia ser
descoberta numa escala muito maior. "O arquiteto neolítico tardio",
escreveu MacLellan Mann em Archaic Sculpturings, "quando projetava, por
exemplo, a planta baixa dos montes de pedra de Caithness, possuía essas
mesmas noções curiosas. Estudei cuidadosamente as suas plantas baixas e
elas mostram, exatamente como os cortes das rochas, o arco do círculo
representado pelas estruturas laterais e a curva de uma elipse em cada final do
monumento (...) os grupos aparentemente isolados, os grupos de pedras eretas
muito distantes umas das outras e os conjuntos de en talhes de rochas
destacados uns dos outros podem fazer parte de um desenho mais amplo".
Em 1937, durante escavações para obtenção de areia perto de
Knappers, a sete milhas da cidade de Glasgow, foram descobertos os
remanescentes de um antigo templo de madeira. Esses restos chamaram a atenção
de MacLellan Mann. Ele os analisou, e também a paliçada serpentina a ele
associada, e descobriu que seu desenho era comparável em escala maciça aos
sinais de cálices e de anéis que havia estudado.
Em The Druid’s Temple near Glasgow, publicado em 1937,
MacLellan Mann escreveu: "O esboço da área é sistemático e exato. Interpretando-se
as dimensões lineares e angulares em períodos astronômicos recorrentes, cada
figura de serpente pode ser identificada, a partir do comprimento de sua linha
medial, com um ou outro dos corpos celestes - o Sol, a Lua e os cinco planetas
-, ou com o espírito do mal do Ano do Eclipse. As várias paliçadas circulares
parecem representar os períodos astronômicos principais, tais como o ciclo
luni-solar de 19 anos ou o Ciclo Saras de 18 anos de 10 1/2 dias, ao final dos
quais podem ocorrer os eclipses".
O "Templo dos Druidas" foi objeto de um grande
interesse, mas o advento da Segunda Guerra Mundial impediu qualquer preservação.
Na época de MacLellan Mann, todavia, por causa da falta de recursos, pesquisas
acuradas e análises de estruturas antigas não foram efetivadas em número muito
grande. Até os estudos do Professor Thom, que o envolveram pessoalmente na
pesquisa de centenas de sítios megalíticos nas llhas Britânicas e na Bretanha,
sentimentos como aqueles expressos por MacLellan Mann podiam ser rejeitados
pelas mentes conservadoras como fantasistas. As formas excêntricas, visíveis na
maioria dos "círculos" de pedras, eram geralmente atribuídas à
incompetência dos seus construtores, que eram vistos, pelos cientistas da
escola vitoriana, como selvagens de parco intelecto, muito pouco superiores aos
macacos. O bom senso nos diz, entretanto, que técnicos que podiam transportar
enormes pedras por distâncias consideráv'eis (por exemplo, o arenito cinzento
de Mynydd Preseli, em Gales, levado para Stonehenge) achariam fácil demais
traçar um círculo verdadeiro.
Todavia, as geometrias exigidas para a construção de observatórios
para o estudo e a documentação dos fenômenos variáveis dos céus são muito mais
complexas do que o traçar um simples círculo. Assim, formas mais complexas
foram utilizadas.
Os grandes conjuntos megalíticos da Grã-Bretanha antiga, e
certamente os círculos menores de pedras que pontilham as charnecas e as
regiões inabitadas do país, foram conclusivamente demonstrados pelo Professor Thom
terem sido planejados com precisão espantosa. Essa geometria exata envolveu o
uso de triângulos retos integrais (triângulos "pitagóricos")
executados com uma medida constante notável - 82,90 cm -, que Thom denominou de
jarda megalítica (JM).
Os círculos de pedra excêntricos, longe de serem sintomáticos
da falha técnica dos seus construtores, foram construídos de acordo com regras
básicas específicas, baseadas em triângulos integrais. Os "círculos"
Tipo 1 de Thom são de fato anéis em forma de óvo, baseados em dois triângulos
retos 3:4:5 colocados um contra o outro. Outro "círculo" comum, o
Tipo 2, também é baseado em dois triângulos 3:4:5, mas desta vez com uma
hipotenusa comum. Outro, de organização mais complexa, segundo Thom, era
produzido a partir de outros triângulos retos integrais tais como 5:12: 13 ou
8:15:17. Stonehenge é um amálgama complexo de círculos e elipses perfeitas e
também pode ser analisado em termos de geometria convencional.
As pesquisas de MacLelÍan Mann e as descobertas complemen tares
posteriores de Thom de linhas de visão do horizonte a partir de círculos de
pedras ou de outras marcas com a intenção de observação celestial e registro
mostram o estágio seguinte do desenvolvimento do microcósmico para o
macrocósmico, No começo deste século, Boyle Somerville e Sir Norman Lockyer
haviam notado esses alinhamentos, mas, até os estudos exaustivos de Thom, eles
não haviam passado de boas hipóteses.
Lockyer é mais bem conhecido por seu trabalho em Stonehenge e
seus arredores, o distrito posteriormente estudado pela escola alemã de
pesquisa geomântica. Durante as suas investigações, descobriu que a tão
conhecida linha do nascer-do-sol do alto verão, que é marcada em Stonehenge
pela famosa Pedra do Calcanhar, era apenas parte de um alinhamento maior de
sítios antigos. Pesquisando a avenida que marca a posição do nascer-da-sol no
dia mais longo do ano, quando contemplada do centro do círculo, Lockyer notou
que ela se alinhava com a terraplenagem antiga de Sidbury HilI. Quando prolongada
na direção oposta, essa linha se alinhava com Grbvely CastIe e com Castle
Ditches, também terraplenagens antigas. Esse alinhamento fora notado
anteriormente pelo Coronel Johnstone, então Diretor Geral de Reconhecimento da
Artilharia. A linha fora utilizada num reconhecimento aperfeiçoado do distrito,
que levou a um aumento da exatidão dos mapas de Reconhecimento da
Artilharia.
A seção entre Grovely Castle e Stonehenge, que tem aproximadamente
seis milhas de extensão, pareceu a Lockyer formar um dos lados de um triângulo
eqüilátero cujo ápice está no sítio da antiga cidade de Old Sarum, também uma
terraplenagem antiga. Old Sarum está no alinhamento Stonehenge-Old
Sarum-Salisbury CatedralClearbury Ring-Frankenbury. Assim, o esboço de
Stonehenge, cuja geometria foi desenhada segundo fatores celestiais, está
integrado com a geometria da paisagem artificial do país, de acordo com as
posições de outras terraplenagens antigas, e é definido por suas localizações
e as define.
Stonehenge combina muitas geometrias num esquema magistral.
Relacionada a fenômenos celestes e ao território vizinho, está situada num
ponto geomântico chave em relação à geometria de toda a paisagem da Inglaterra
meridional. O henge está situado sobre muitas linhas ley importantes, incluindo
uma que parte da torre da igreja de St. Michael, que está no alto de
Glastonbury Tor. Este ley, que vai de Glastonbury Tor até um túmulo situado em
Deerleap Wood, perto de Dorking, no Surrey, passando por St Michael, Gare Hill,
Maiden Bradley Priory, Stonehenge e Shere Church, é, como a linha do pôr-do-sol
em Stonehenge, uma extensão do lado de uma figura geométrica de vastas
dimensões. Nesse caso, é a extensão do lado de um decágono que liga pontos
geomânticos vitais aos de um outro.
A geometria do henge, em si mesma, baseada no eixo
solsticial, apresenta uma tendência à divisão sêxtupla. Este fato foi
percebido desde a época de Inigo Jones (1652) e evocou comentários
de místicos do porte de John Wood, Hermon Gaylard Wood e John Michell. A
descoberta de Lockyer de um triângulo eqüilátero com lados que medem seis
milhas liga a geometria sagrada sêxtupla microcósmica à geometria da paisagem
macrocósmica.
Lockyer, todavia, foi apenas um numa longa linha de pesquisadores
que estudaram o alinhamento de sítios antigos. Entre 1870 e 1872, um perito em
estradas romanas chamado William Henry Black tornou pública uma teoria
surpreendente. Ele persistiu em seus estudos por cinqüenta anos antes de
liberar os seus resultados a um público insensível e incrédulo. Black pretendia
ter descoberto nada menos do que todo um sistema de "grandes linhas
geométricas", radiais e poligonais, que cruzavam toda a Grã-Bretanha e
avançavam para além dela. Elas ligavam de maneira precisa os maiores marcos de
fronteiras, chegando a definir inclusive os marcos limítrofes dos municípios.
Anteriormente, esse conceito nunca fora corrente. Além de uma
referência que se encontra num obscuro livro ocultista publicado em 1846 -
feita em relação a uma linha de terraplenagens antigas em Wiltshire -, até
mesmo os alinhamentos não haviam recebido apoio algum.
Blafk morreu em 1872, mas nenhum sucessor chegou a elabora!
ou mesmo corroborar suas descobertas. Todavia, ele não deixou de exercer
influências.
Seu maior comentário sobre as "grandes linhas
geométricas" foi feito em Hereford em 1870 durante uma viagem de campo da
Associação Arqueológica Britânica. O encontro em que Black fez sua exposição
foi presidido por uma personalidade local, o Dr. BulI, do Clube dos
Naturalistas de Woollhope. Nos anos que se seguiram à morte de Black, Bull
mencionou a sua obra em muitas ocasiões. A um desses encontros estava presente
um moleiro e pioneiro fotográfico interessado em antigüidades - Alfred
Watkins.
Cinqüenta anos após Black ter falado em Hereford, Watkins
anunciou que fizera uma descoberta momentosa - alinhamentos de sítios antigos,
aos quais deu o nome de "leys". Watkins, como Black e outros antes
dele, descobriram que as terraplenagens antigas, os marcos fronteiriços, as
igrejas e outras espécies de monumentos antigos estavam arranjados em linhas
retas. Com seus livros Early British Trackways, The Old Straight Track e
Archaic Tracks Around Cambridge, Watkins tornou-se o expoente mais conhecido
dos sítios alinhados, o pai dos "caçadores de ley", como são conhecidos
os seus seguidores. Diferentemente de Black, que ensinava que as
suas "grandes linhas geométricas" eram os remanescentes de uma
inspeção antiga, Watkins considerava que os seus alinhamentos eram os resíduos
de uma antiga rede de veredas.
Watkins apenas arranhou a superfície dos alinhamentos orientados
e nem chegou a tocar o relacionamento dos centros radiais com a geometria. Isto
parece estranho, pois Watkins certamente ouvira falar de Black e deve ter
conhecido a obra de MacLellan Mann, que mencionara "pedras (...) num
relacionamento geométrico exato". De qualquer forma, Watkins dedicou o
resto de sua vida a disseminar as suas idéias sobre os alinhamentos. Embora
tenha morrido em 1935, foi só nos últimos quinze anos que sua obra tornou-se
conhecida e estudos baseados nela, especialmente os de Paul Devereux e Ian
Thomson, verificaràm muitas das suas descobertas.
Watkins e a sua escola ignoravam em grande medida a obra de
Lockyer, que exercera mais impacto na Alemanha do que em sua nativa Grã-Bretanha.
Pouco tempo após a publicação de seu livro Stonehenge and Other British
Stone Monuments Astronomically Considered (1909), um pesquisador alemão chamado
Albrecht publicou uma discussão sobre o significado astronômico de Stonehenge
no periódico Das Weltall (O Universo). A sua fonte inicial foi Lockyer. Pouco
tempo depois, Albrecht foi morto na Primeira Guerra Mundial, mas, em 1920, o
Padre Leugering leu seu livro e começou a procurar sistemas similares na
Vestfália, onde nascera.
A derrotada Alemanha dos anos 1920 era um terreno fértil para
os sentimentos revolucionários e chovinistas e os estudiosos da "geografia
sagrada", como se dizia então, encontraram seu refúgio. O colaborador de
Leugering, Josef Heinsch, advogado e projetista regional, descobriu
alinhamentos do tipo dos de Stonehenge por toda a Alemanha. Em suas pesquisas,
estudou a geografia sagrada e seu aspecto microcósmico, a geometria sagrada,
que demonstrou serem dois aspectos da mesma disciplina geomântica.
O paladino principal da cultura germânica antiga foi Wilhelm
Teudt, que, mais que todos os outros, devia tornar-se a figura de proa da
ciência da geometria da paisagem. Em seu grande livro Germanische Heiligtümer
(Santuários alemães antigos), publicado em 1929, anunciou a sua descoberta de
alinhamentos aos quais denominou heilige linien (linhas sagradas). Estas,
segundo ele, baseavam-se em fenômenos astronômicos. Na Teutoburger Wald,
floresta que é o coração místico da Alemanha, sítio de muitas façanhas legendárias
e heróicas, Teudt estudou as orientações das terraplenagens hexagonais
irregulares de Haus Gierke, em Oesterholz. Essas terraplenagens estavam
situadas ao redor de uma cabana de caça do século XVII, mas Teudt pretendja que
as terraplenagens fossem os resíduos de um antigo observatório astronômico. As
orientações das terraplenagens foram testadas por astrônomos profissionais, que
descobriram que elas' foram alinhadas em suas posições, segundo muitas
características astronômicas, em 1800 a.C. Heinsch tomou a liberdade de discordar,
afirmando que as formas das terraplenagens, embora antigas, estavam
determinadas pela geometria sagrada.
As heilige linien de Teudt, que ligavam sítios
significativos, embora fossem primordialmente astronômicas, eram similares em
conceito às linhas geométricas de Black e às leys de Watkins. A partir de uma
terraplenagem qualquer mais antiga, Teudt descobriu que deveria existir pelo
menos uma marca de orientação na forma de uma "torre de relógio"
situada ao longo do eixo norte-sul ou leste-oeste. As linhas ligavam sítios
sagrados em relações geométricas significativas, estando elas próprias ligadas
a fenômenos astronômicos.
No final dos anos 1930, a obra de Teudt e de seus colegas foi
retomada por alguns nazistas e a ela foi propiciado um apoio oficial que
possibilitou que os pesquisadores produzissem um amplo conjunto de material
sobre a geometria da paisagem. Josef Heinsch descobriu um vasto sistema
interligado de alinhamentos e de figuras geométricas com distâncias e ângulos
significativos que cobriam seções amplas do vale do Reno. Como os pesquisadores
geomânticos anteriores, descobriu que a geometria da paisagem era freqüentemente
uma versão ampliada da geometria de sítios individuais, estabelecendo um
vínculo físico entre o microcosmo e o macrocosmo. Heinsch viu a sua descoberta
como "um templo sagrado indestrutível da natureza", que era o continuum
da geometria sagrada em círculos e templos de pedras sem o esboço da paisagem.
Com a destruição da Alemanha nazista, todas as pesquisas geomânticas
alemãs cessaram. A obra de Teudt e dos seus seguidores foi esquecida, até que
os pesquisadores geomânticos ingleses a redescobriram nos anos 1970. Muito da
obra de Heinsch e de seus colegas tem saído agora em tradução inglesa e se
transformou nos dados mais detalhados e mais convincentes coletados até agora.
Uma nova geração de pesquisadores está agora estudando a
geometria da paisagem. Em seu livro City of Revelation, John MichelI revelou a
existência de uma grande figura geométrica na Grã-Bretanha meridional. Os
três antigos "coros perpétuos" celtas de Llantwit Major, Glastonbury
Abbey e Stonehenge, segundo esse pesquisador, formam três vértices de um
decágono regular de proporções majestosas. Existe um quarto vértice em
Goring-on-Thames, onde havia antes um grande templo pagão na junção de muitas
veredas importantes. O centro desse vasto decágono está na aldeia de
Whiteleaved Oak, na qual se reuniam os antigos municípios de Hereford,
Gloucester e Worcester. Esse decágono relaciona-se em ângulos e em distância a
outros centros geomânticos da Grã-Bretanha, sobre os quais muito se tem
escrito ultimamente.
Os pesquisadores, de Black a Michell, encontraram os padrões
antigos fixados ,indelevelmente na paisagem. As linhas que ziguezagueiam pelo
país têm obviamente a mesma antigüidade dos círculos de pedra, mas as igrejas
cristãs mais modernas e as granjas podem ser invariavelmente enquadradas no
mesmo modelo. Todas essas descobertas - tanto na escala das gravações em pedra
e nos círculos feitos com esse material quanto através de toda a extensão da
paisagem - apontam para a existência de uma civilização mais antiga, agora
completamente desaparecida, cuja tecnologia espiritual da geometria não foi
superada. Sua importância pode ser avaliada pela sobrevivência de seu
conhecimento nas escolas de mistério da Idade Média.
Podemos, assim, traçar uma linha progressiva em que as primitivas
gravações em rocha de antigüidade inimaginável levam, com a astronomia, à
construção de observatórios de pedra complexos e sofisticados que também
estavam ligados a uma matriz geométrica mais ampla. Por imposição da
religião cristã, esses sítios foram freqüentemente apropriados pelas igrejas.
Todavia, as orientações e as posições foram preservadas e a geometria estava
diretamente relacionada à estrutura antiga. O Professor Lyle Borst demonstrou
em seu livro Megalithic Software que os padrões geométricos que subjazem às
capelas orientais das catedrais de Wells, Lincoln, Canterbury, Gloucester,
Winchester e de muitos outros lugares derivaram da geometria megalítica
exposta por Thom e, portanto, indicam a presença naqueles locais de círculos de
pedras. Nos casos das catedrais góticas e românicas, os geômetras fizeram uma
síntese da geometria megalítica antiga com o ad triangulum e o ad quadratum
maçônicos. A geometria dos céus, traduzida na pedra, foi novamente transmutada
para o serviço de outros deuses, mas permanece até hoje reconhecível para
aqueles que sabem o que devem buscar.
4. A Geometria Sagrada
Egípcia Antiga
Geometria significa literalmente "medição da terra"
e seu desenvolvimento no Egito antigo deveu-se precisamente a esse objetivo.
Numa data muito recuada no tempo, possivelmente há cinco ou seis mil anos, os
egípcios desenvolveram um esquema empírico de agrimensura do solo. O esquema
básico nasceu da necessidade de se evitar que o transbordamento anual do rio
Nilo destruísse todas as fronteiras. Com a criação do governo centralizado, e a
fim de assegurar uma taxação eqüitativa e evitar disputas, as fronteiras tinham
de ser restabelecidas depois de cada inundação. Necessariamente, o método de
agrimensura tinha de ser praticável e simples. Não exigia mais que dois homens
e uma corda cheia de nós, além do conhecimento do chamado triângulo
"pitagórico", séculos antes que Pitágoras caminhasse por este mundo.
O traçado das áreas requeria um método seguro para a produção
do ângulo reto. . Este era conseguido por intermédio da divisão de uma corda em
treze divisões iguais. Quatro unidades formavam um lado de um triângulo, três o
outro e mais cinco constituíam a hipotenusa oposta ao ângulo reto. Esse método
simples persistiu até os nossos dias e foi utilizado quando se deu início à
construção de túmulos e templos. Foi a origem da histórica "cordagem do
templo" e, a partir dessa técnica, era relativamente simples a tarefa de
esboçar retângulos e outras figuras geométricas mais complexas.
Enquanto se desenvolvia, toda a antiga cultura egípcia mesclou-se
tão completamente à religião canônica, que quase todos os atos eram formalizados
num ato de adoração. Os templos e a arte dos túmulos são os melhores exemplos
dessa vida sagrada rigidamente organizada. Cerimônias mágicas complexas
resultaram de importantes eventos de estado em que o monarca dirigente
representava o papel de personificar uma divindade. No planejamento dos
templos, a formação básica da geometria subjacente era executada numa complexa
cerimônia simbólica.
Em The Dawn of Astronomy, Sir Norman Lockyer observou que a
"cordagem do templo", que o esboçava por meio de uma corda, era
acompanhada de um cerimonial comparável ao da moderna deposição da pedra
fundamental. Ele cita descrições do processo tomadas das inscrições murais de
Edfu, Denderah e Karnak. "Ascendeu o rei", diz uma dessas
inscrições, "vestido com seu colar e sua coroa emplumada; e o mundo todo o
seguiu, e a majestade de Amenemhat. O ker-heb (Sumo Sacerdote) leu o texto
sagrado durante o estiramento da corda de medição e da deposição da pedra
fundamental no pedaço de chão escolhido para esse templo. Retirou-se então sua
majestade Amenemhat e o rei Usertesen a inscreveu no solo diante do povo".
A corda tinha uma função dupla: fixar a orientação do templo
por observação direta de um objeto celestial e também, a partir daí, esboçar
por meio da geometria o padrão sagrado do próprio templo. Outra inscrição diz:
"O Deus vivo, o filho magnífico de Asti, alimentado peja sublime deusa no
templo, o soberano do país, estira a corda com alegria, com seu olhar voltado
para o ak da constelação da Mão do Touro, estabelece a morada-templo da senhora
em Denderah, como já ocorreu antes". Esta é uma referência aos dois
templos da Deusa em Denderah, um consagrado a Ísis e o outro a Hathor.
Após fixarem a orientação segundo a constelação da Mão
do Touro (agora conhecida como do Arado ou Ursa Maior), os cordoadores
estabeleciam uma linha em ângulo reto em relação a ela por meio da criação de
um triângulo 3:4:5 e, a partir dele, esboçavam todo o templo.
Ao longo de toda a história registrada, a forma retangular representou
o corpo do homem e, por correspondência microcósmica/ macrocósmica, os céus.
Sua forma complementar, o padrão geométrico central ou radjal, igual em todas
as direções e emblema do mundo material, foi admiravelmente representado no
Egito pelas pirâmides.
A construção das pirâmides foi levada a efeito num período relativamente
curto. Embora sejam conhecidas cerca de sessenta pirâmides, as maiores e mais
famosas do grupo de três situadas em Giza, perto do Cairo, têm sido, mais do
que quaisquer outras, objeto de escrutínio e de especulação. Testemunhos de
autores antigos, tais como o do grego Heródoto, que viveu no século V a.C., confirmam
que a função primária das pirâmides era servir de sepulcro.
Os reis egípcios, que reuniam em suas pessoas as funções de
sacerdote, rei e deus, esforçaram-se durante todas as suas vidas terrenas para
se munirem de túmulos custosos que assegurassem a sua sobrevivência no
pós-vida.
Heródoto menciona brevemente o extenso período de construção
da Grande Pirâmide e afirma que ela era a tumba do rei Quéops. De acordo com O
historiador, foi erigida sob as ordens do rei durante a sua vida de vaidade
despótica e com o intuito de perpetuar a sua memória para sempre.
Quatro séculos após Heródoto, o grande historiador e geógrafo
Diodoro Sículo visitou as pirâmides e nos deixou o seguinte relato: "A
maior delas", escreve Diodoro. "é quadrangular, cada lado mede
setecentos pés de extensão em sua base e mais de seiscentos de altura;
contrai-se gradualmente no topo, onde cada lado tem seis côvados; está
construída inteiramente em pedra sólida, de difícil artesania, mas duração
externa; pois nos mil anos que se diz terem transcorrido desde a sua
construção, as pedras, que alguns dizem ser mais de três mil e quatrocentas,
nunca foram movidas de suas posições originais e o todo permanece indene".
O vasto volume e a impressionante geometria das pirâmides
fizeram que muitos cronistas e comentadores antigos a elas se referissem em
suas obras. O geógrafo grego Estrabão (c. 63-25 a.C.) visitou-as e o soldado-cientista
romano Plínio, além de escrever sobre as pirâmides, mencionou outros autores
que haviam escrito sobre elas; Euheferus, Aristágoras, Duris de Sarnos,
Antístenes (o filósofo negativista), Demétrio, Demóteles e Apião. Todas as suas
obras sobre as pirâmides estão perdidas, o que nos faz lembrar quão
fragmentárias são as fontes escritas da história de que dispomos no presente.
Nosso interesse, contudo, está nos princípios da geometria
sagrada subjacente à estrutura desta e de outras pirâmides. A Grande Pirâmide
pode ser vista como o ápice de uma tradição que começou com a Pirâmide Escada
do rei Zoser em Saqqara (c. 2.750 a.C.). Muitas outras pirâmides são anteriores
à Grande Pirâmide e seus desenhos apresentam um padrão evolutivo que culminou
na própria Grande Pirâmide. Depois, a tradição declinou e uma série de
pirâmides abastardadas foi construída, muitas das quais se desintegraram
devido a um acabamento inferior.
A primeira pirâmide verdadeira, o túmulo do rei Zoser em
Saqqara, foi desenhada por Imhotep, um homem de gênio tão excepcional, que,
após a sua morte, foi elevado à condição do deus que fundamentou a medicina e a
arquitetura. A Pirâmide Escada tinha uma planta baixa quadrada e, como os
zigurates babilônicos, era mais uma "montanha sagrada" em forma de
escada do que uma pirâmide de lados nivelados. Estava contida num vasto santuário
que tinha a forma de um quadrado duplo cercado por uma parede de 30 pés. O
santuário, um empreendimento grandioso em si mesmo, tinha 1.788 pés de
comprimento - um terço de milha - e estava orientado no eixo norte-sul. A forma
desse cercado forneceu o padrão dos lugares sagrados posteriores. Foi usada,
inter alia, séculos depois, no Tabernáculo e no Templo dos Judeus, e também
como o padrão subjacente da Capela Real de Whitehall, em Londres.
A Pirâmide Escada representa uma aplicação repentina de mé todos
que parecem ter sido desconhecidos anteriormente. A tecnologia do corte da
pedra e do transporte era conhecida, mas nunca fora tentado um empreendimento
dessa grandeza. No pátio da Pirâmide Escada havia uma estátua em cujo plinto
estava o nome de Imhotep com a citação "Chanceler do Rei do Baixo Egito,
Primeiro após o Rei do Alto Egito, Administrador do Grande Palácio, fidalgo
hereditário, Sumo Sacerdote de Heliópolis, Construtor, Escultor e
Fabricante-em-chefe de Vasos". Lista tão impressionante de posições
oficais realça o excepcional talento desse homem que, acima de todos os outros,
encabeça a Tradição Ocidental da geometria sagrada.
Imhotep era filho de Ka-nefer, Diretor de Obras do Alto e
do Baixo Egito, não um homem de sangue real. Todavia, a lista
de títulos de sua efígiee os atributos que lhe foram concedidos
após sua elevação ao panteão demonstram a unidade essencial de
magia, religião e tecnologia egípcias antigas. A descoberta da tumba
dessa figura seminal foi durante muito tempo um sonho acalentado
pelos egiptólogos. Acredita-se que esteja em algum lugar nos
arredores de Saqqara, mas até hoje permanece inviolado o local de repouso do
originador da arquitetura no Ocidente.
Após a pirâmide de Zoser, uma outra foi iniciada em
Saqqara pelo rei Sekhemket. Por alguma razão desconhecida, foi abandonada
a uma altura de apenas vinte pés; uma terceira pirâmide de degraus, em Zawiyet
el Aryan, que se acredita ter sido ordenada pelo rei Khaba, também foi
abandonada durante a construção. Depois dessas pirâmides de degraus, foram
erigidas pirâmides verdadeiras revestidas de lajotas polidas feitas de
calcário de Tura.
A primeira das pirâmides verdadeiras, a do rei Sneferu, em
Meidum, foi um desastre. No seu livro The Riddle of the pyramids, Kurt
Mendelssohn mostrou, a partir da configuração do cascalho que circunda o centro
dessa pirâmide em ruínas, que ela desmoronou durante a construção. O
acabamento imperfeito e a natureza' inovadora do projeto causaram um
colapso repentino. Esse desastre, num período em que raramente se viam no
mundo edifícios dessas dimensões, deve ter produzido um efeito profundo sobre o
povo da época e pode ser cultuado em forma deturpada no mito da Torre de BabeI.
Como a pirâmide de Zoser, o modelo de Meidum foi desenhado como uma
pirâmide de degraus, mas foi preenchido com blocos de vedação e de
revestimento. Os poucos blocos de revestimento remanescentes, retirados de uma
caótica pilha de cascalho que cerca essa pirâmide, mostram que o ângulo de
elevação era 52°, Um ângulo de grande importância na geometria sagrada.
Quando a pirâmide de Meidum foi surpreendida pelo desastre,
uma outra pirâmide, em Dahshur, ainda estava em construção. Esta é única
dentre todas as pirâmides que sobreviveram. A parte inferior do revestimento
eleva-se num ângulo de 54º; depois, num ponto situado a meio caminho do
topo, muda abruptamente para 43°30'. É provável que o arquiteto dessa
pirâmide tivesse alterado o ângulo a fim de que o desastre de Meidum não
se repetisse nessa construção.
Todavia, é óbvio, em comparação com todas as outras pirâmides,
que a "Pirâmide Encurvada", como ela é conhecida, representa uma
aberração em relação a uma norma ideal. As pirâmides revestidas representam o
espetáculo celestial dos raios do sol rompendo por entre as nuvens após uma
tempestade - uma manifestação do poder divino de Ra. A mudança total das
pirâmides de degraus inspiradas em Imhotep para a forma pura parece ter ocorrido
na mesma época em que os sacerdotes de Heliópolis passaram a ocupar uma posição
de poder no Egito. Curiosamente, a sua ascendência introduziu uma nova
interpretação da geometria sagrada: a pirâmide verdadeira, o obelisco e o
ben-ben, o pilar cônico sagrado do Templo de Ra, em Heliópolis.
Após o fiasco da Pirâmide Encurvada, a próxima pirâmide,
situada a uma milha ao norte, foi construída com o ângulo inferior de 43°30', o
ângulo da metade superior da sua antecessora. Todavia, nem tudo estava
perdido. As lições dessas três falhas foram analisadas e a construção da maior
estrutura jamais erigida pelo homem foi iniciada: a incomparável Grande
Pirâmide.
A Grande Pirâmide, construí da aparentemente para alojar os
restos mortais do rei Khufu (mais conhecido por Quéops, seu nome grego), foi
edificada com uma planta baixa quase perfeita de 775 pés e um ângulo de
ascensão de 51°52'. Seu volume é um estonteante acúmulo de 6 1/2 milhões de
toneladas de calcário. O ângulo de ascensão dá à pirâmide uma propriedade geométrica
única, que representa a quadratura mística do círculo: sua altura está para a
mesma razão da sua circunferência, assim como o raio para a circunferência de
um círculo. Essa razão é 1/2 pi . pi = 3,1416... e, nessa pirâmide, esse número
transcendental está representado com uma margem de erro de apenas 0,1%.
O ângulo de 51°52' tem a propriedade de ser o ângulo produzido
por um gradiente de 4:1. O ângulo utilizado em Dahshur, 43°30', é preduzido por
um gradiente de 3:1. Assim, a simples utilização de números inteiros, que é a
chave da geometria sagrada, ao longo de toda a história, existe também no
contexto egípcio. "A existência das pirâmides", escreveu James
Stirling em The Canon, "(...) parece ser uma confirmação notável das
afirmações dos escritores primitivos - de que a arquitetura dependeu
originalmente da geometria - e vemos no Egito a primeira aplicação dessa
ciência do construir. (...) Nas mãos dos arquitetos geométricos, a pirâmide -
por seu volume, superfície, linhas e ângulos - poderia fornecer os meios de se
registrar medidas e números. Por objetivos práticos, também, a pirâmide é a
forma mais adequada para uma estrutura permanente"'.
Outra característica geométrica das pirâmides que tem
sido muito comentada diz respeito às suas faces. Tem sido muito discutida
a teoria de que as pirâmides foram concebidas como representações do
hemisfério setentrional em projeção quadrada. Cada face plana da pirâmide
deve representar um quadrante curvo desse hemisfério, segundo essa teoria.
A pirâmide cumpre essa consideração geométrica como nenhuma outra figura: para
se projetar um quadrante esférico num triângulo plano, a base do quadrante
deve ser igual à base do triângulo e deve ter a mesma altura. A
Grande Pirâmide cumpre essas determinações, pois que o ângulo de incli nação
dá a relação pi entre a altura e a base.
As complexidades da geometria inerente à Grande
Pirâmide têm sido amplamente desemaranhadas numa pletora de cálculos
e de teorias desde o último século. Heródoto soube pelos sacerdotes do
Templo que a Grande Pirâmide foi construída de maneira que a área de cada
face fosse igual ao quadrado da sua altura. Essa relação parece incorporar
a Seção Dourada, que, de acordo com o geômetra moderno Schwaller de
Lubicz, não foi vista em termos numéricos mas como emblema da função criativa
ou geradora, fundamento de uma série infinita.
No interior da Grande Pirâmide há uma enigmática série de passagens
cuja intenção ainda não pôde ser determinada. Ela compreende três câmaras: a
Câmara do Rei, que contém apenas um sarcófago vazio; a Câmara da Rainha,
que é menor e também está vazia; e uma câmara inacabada escavada na rocha viva
ao nível do solo. Além dessas três câmaras, há uma passagem impressionante conhecida
como Grande Galeria, alinhada com um revestimento de granito cuidadosamente
executado e dotada de um teto finamente mi sulado. Todavia, nunca se
descobriu na Grande Pirâmide nada que fosse digno de menção -
característica que forneceu aos piramidólogos farta munição para as suas
teorias sobre armazéns e observatórios.
Hubert Paulsen, arquiteto dinamarquês, desorientado pela
faIta de conteúdo, pretendeu que exista uma outra câmara na Grande Pirâmide que
ainda não foi descoberta. Recorrendo à geometria, ele calculou que a verdadeira
câmara sepulcral, tão abarrotada de riquezas que poderia ofuscar os
tesouros de Tutankhamun - um monarca pobre em comparação a Khufu -,
deveria estar próxima do centro da pirâmide e abaixo do nível do solo. A Câmara
do Rei - que se poderia imaginar destinada a conter os requisitos necessários à
vida pós-morte do Faraó, além do fato de estar a 130 pés acima do nível do solo
- não está exatamente na direção do ápice da pirâmide. A câmara de Paulsen,
infelizmente, não foi localizada, e experiências levadas a efeito na Pirâmide
de Khafre (Quefrem) também resultaram em fracasso.
Comparada à Grande Pirâmide, cujas câmaras e passagens foram
reveladas pela queda acidental de um bloco do teto na passagem da entrada, a
Pirâmide de Khafre aparentemente não possui passagens. Há uma câmara pequena,
na rocha situada abaixo do vasto volume da estrutura. Ela sempre pareceu
anômala aos olhos dos egiptólogos, e uma tentativa de obter um
"raio-X" da pirâmide foi feita em 1970 pelo Professor Luis Alvarez,
da Universidade da Califórnia. Alvarez tentou registrar a passagem pela
pirâmide de raios cósmicos, que chegam à Terra vindos do espaço. Usando um
equipamento de detecção extremamente sofisticado, fez observações que
abrangeram um período de muitos dias. Na análise dos resultados, os raios
apresentaram variações inexplicáveis que tornaram inconclusivo o experimento. A
variabilidade dos resultados talvez fosse causada pela geometria da pirâmide,
seu posicionamento, sua relação com o campo magnético da Terra ou alguma
combinação desses e de outros fatores. Seja qual for a causa, o experimento de
Alvarez não conseguiu detectar quaisquer câmaras internas ou passagens.
Muitas asseverações extravagantes foram emitidas no sentido
de se interpretar a complexa disposição das passagens e de outras
características internas da pirâmide de Khufu, mas na verdade nenhuma delas
merece mais atenção do que as outras. Dignas de nota são aquelas teorias de que
o Segundo Advento de Cristo, o fim do mundo ou outro acontecimento momentoso
estão pressagiados por vários degraus, várias junções de pedras, vergas de
passagens e fissuras. Os livros sobre profecias da pirâmide apresentam a
infeliz tendência de exigirem uma revisão drástica quando o apocalipse
profetizado não ocorrer no tempo previsto. Que o leitor julgue a validade da
obra de Piazzi Smith, John Taylor, John Davidson, Edgar Stewart, Basil Steward
e seus imitadores.
Embora as pirâmides sejam a manifestação mais augusta da
geometria sagrada no Egito, suas artes canônicas geometricamente inspiradas impregnaram
todos os artefatos sagrados. O título de "Fabricante-em-chefe de
Vasos" dado a Imhotep demonstra que se exigia um grande geômetra para o
desenho correto e a manufatura de utensílios sagrados. Produtos da arte
egípcia de qualquer período são, com poucas exceções, reconhecidos
instantaneamente como tal. O estilo foi praticado por mais de 3.000 anos, até
mesmo durante o período helênico posterior à conquista do país por Alexandre o
Grande. As medidas canônicas e o sistema proporcional, considerados como
expressões de um ponto de vista mágico do mundo, inibiram qualquer inovação. O
papel do artista era, então, bastante diferente do de sua contrapartida
moderna. O conceito do artista como uma personalidade criadora individual é
absolutamente moderno. Como outros artesãos, a maioria dos escultores e pintores
fazia parte de um grupo que aderia rigidamente aos cânones artísticos ordenados
previamente. Sua posição pode ser comparada à dos desenhistas modernos de
circuitos impressos ou microprocessadores, que estão aprisionados a uma
estrutura tecnológica de função que depende apenas das leis da eletrônica.
A exemplo das suas contrapartidas tecnológicas modernas, os
artesãos do Egito antigo eram trabalhadores de precisão, os praticantes
primitivos da crença universal de que os atos de magia devem ser realizados
segundo um ritual preciso e imutável. A geometria subjazia a essas formas
rituais.
A base técnica da geometria egípcia era impecável. Na verdade,
o sucesso posterior dos gregos antigos, com os quais hoje se associa
prontamente a geometria, estava solidamente baseado no conhecimento e na
técnica dos egípcios antigos. As práticas da geometria egípcia não estão perdidas,
todavia, pois o grande despertar do interesse pelas antigüidades do Egito
durante o último século levou à redescoberta dos seus fundamentos. Durante
as escavações destruidoras da estrutura da Grande Pirâmide, o Coronel Howard
Vyse descobriu em uma das câmaras "muitas marcas similares às que foram
encontradas em outras câmaras e também muitas linhas vermelhas que se cruzavam
em ângulos retos, com triângulos eqüiláteros em preto, traçados ao lado da
'intersecção'. talvez com o objetjvo de se obter um ângulo reto". Essas
linhas e essas construções eram necessárias às artes maçônicas do corte da
pedra, sua preparação e seu acabamento. Para qualquer método técnico de esboço,
é necessário possuir uma base geométrica. O uso de linhas de intersecção para
marcar o plano de fundo de um entalhe foi sistematizado numa grade quadrada.
Essa grade era um auxílio não só para a composição geral e para o desenho da
obra, mas também servia para assegurar que as figuras humanas fossem executadas
segundo as proporções corretas prescritas pelo cânone.
As linhas mestras eram pintadas com um pincel ou feitas com
um cordão molhado em tinta vermelha e os traços eram esboçados com um pincel
feito de fibras vegetais ou um pincel de junco semelhante aos usados pelos
escribas. O escultor cinzelava ao redor dos esboços e a escultura era então
concluída com uma cobertura de gesso. Finalmente, era pintada com cores
canônicas. Retângulos de raiz eram utilizados para determinar as dimensões
principais das figuras numa estrutura originalmente quadrada. Assim, a
simetria dinâmica impregnou-se canonicamente na escultura que reproduzia em
suas dimensões todos os atributos sagrados da geometria. Isto se acrescentava
ao seu conteúdo figurativo e simbólico. Esses retângulqs eram facilmente
construídos por geometria simples a partir de uma grade quadrada que
também possuía o significado simbólico do mundo, de que o homem era o Templo. A
geometria fundamental da fundação do Templo era reproduzida microscopicamente
em cada entalhe canônico, segundo as fórmulas antigas do corpo do Templo.
característica que podemos encontrar ao longo de toda a história registrada da
arquitetura.
Essa combinação de grade subjacente, de geometria sobrejacente
e de forma externa é um conceito trifacetado da arte sagrada sem o qual as
formas múltiplas mal podem ser compreendidas. Esse conceito três-em-um,
encapsulado na Trindade-de Ísis, Horus e Osíris, ocorre ao longo de toda a arte
canônica do Egito para a frente. Numa arte sagrada pode predominar a forma
geométrica. tal tomo nas obras célticas ou nos padrões de azulejos islâmicos.
Trata-se de manifestação do segundo nível. Em geral, a manifestação visível da
forma é suprimida. Essa geometria tem a característica de incorporar em si
mesma a metrologia sagrada do sistema qualquer que ela representa.
Uma característica da geometria sagrada que torna a ocorrer
ao longo do tempo é a escolha de geometrias que são tão inclusivas quanto
possível. Uma geometria que inclui o quadrado, o círculo. o vesica e o
triângulo equilátero, bem como vários retângulos de raiz e a Seção Dourada, tem
sido considerada como o microcosmo ideal. A tumba do rei Ramsés IV do Egito é
um exemplo típico. Ramsés foi enterrado numa tumba cavada na rocha. não numa
pirâmide, pois a construção da pirâmide foi abandonada. A tumba cavada na rocha
continha um sarcófago triplo. O sarcófago interior tinha a forma de um
quadrado duplo, o mais santo dos recipientes sagrados. Ao redor dele, o
sarcófago intermediário tinha as dimensões de um retângulo da Seção Dourada, ao
passo que o sarcófago externo possuía dois retângulos da Seção Dourada
iguais ao do sarcófago intermediário. A tumba foi dimensionada numa
projeção da geometria desse sarcófago triplo. Essa geometria harmônica, levada
a um grau de perfeição altíssimo pelos gregos antigos, foi aplicada em toda a
arte sagrada egípcia.
Os peitorais e outros amuletos mágicos encontrados em
egípcios mumificados foram analisados geometricamente. Eles exibem essa
geometria que congrega o quadrado duplo e a Seção Dourada, fato que demonstra a
unidade da geometria sagrada egípcia desde o maior até o menor objeto sagrado.
5. A Geometria Sagrada
Mesopotâmica e Hebraica
Embora o relato bíblico da destruição da Torre de Babei
talvez seja uma lembrança popular deturpada do colapso que ocorreu durante a
construção da Pirâmide de Meidum, a tradição da edificação de montanhas
sagradas artificiais encimadas por templos tem raízes sem dúvida na Babilônia.
Seja qual tenha sido a origem desse colapso lendário, havia com certeza na
Babilônia um zigurate cujas dimensões e cuja geometria têm sido reconstruídas
com o auxílio de evidências documentais e arqueológicas. Desenhadas como
reproduções miniaturizadas do arranjo do universo, essas montanhas sagradas
estavam orientadas para as quatro direções cardeais. O nome dado a elas,
ziggurat, significava "pico dos deuses". Estima-se que os zigurates
escavados nas cidades mesopotâmicas de Ur, Uruk e Babilônia mediam trezentos
pés da base até o ápice. O zigurate de Khorsabad media 150 pés quadrados na
hase e 135 pés de altura, desde o pavimento até a plataforma que o encimava.
A estrutura compreendia sete estágios, representando cada um
deles os atributos de um dos planetas e pintado com uma das cores planetárias.
O zigurate de Nabu, em Borsippa (Barsipki), era conhecido como a "Casa dos
Sete Limites do Céu e da Terra" e representava a ligação cósmica que
existe entre os planos terrestre e celestiaI. James Fergusson, em A History of
Architecture in All Countries (1893), escreveu:
"Esse templo, segundo a decifração dos cilindros que
foram encontrados em seus ângulos, era dedicado aos sete planetas ou esferas
celestes e seus estágios foram adornados, em conseqüência, com as cores de
cada um deles. O mais baixo de todos, além de tudo ricamente apainelado, era
preto, a cor de Satumo; o seguinte, laranja, a cor de Júpiter; o terceiro era
vermelho, cor emblemática de Marte; o quarto, amarelo, pertencente ao Sol; o
quinto e o sexto eram verde e azul, respectivamente, dedicados a Vênus e a
Mercúrio; e o último talvez fosse branco, a cor pertencente à Lua, cujo lugar
no sistema caldaico era o mais elevado.”
A ligação cosmológica foi pesquisada pelo Professor
Stecchini, que acredita que o zigurate de sete estágios era uma representação
do hemisfério setentrional da Terra, representando o nível do solo o equador e
o ápice, o pólo. Na geografia grega, a área situada entre o equador e o pólo
era dividida em sete zonas, cada uma menor do que a anterior para compensar o
grau de longitude cada vez menor à medida quc se aproxima do pólo. A alegação
de Stecchini de que o zigurate representava o hemisfério é apoiada pelos
tabletes cuneiformes que afirmam que cada nível do zigurate tinha uma área
específica determinada por unidades padronizadas de medida de terra.
O tablete cuneiforme conhecido como Tablete Smith afirma
especificamente que cada terraço do zigurate da Babilônia possuía sua própria
medida simbólica. Essa diferenciação possibilitou que vários esquemas
geométricos fossem incorporados ao edifício. O terceiro estágio era
particularmente importante, porque foi construído na forma de um quadrado com
lados de seis côvados - uma unidade fundamental da medida babilônica de terra.
O ângulo de elevação em vários pontos produz razões geométricas importantes,
tais como V5 -1, ângulos fundamentais na agrimensura da terra, também encontrados
na Grande Pirâmide.
Hermon Gaylord Wood, um metrólogo bostoniano, analisou a
escrita cuneiforme como parte de sua grande pesquisa sobre a metrologia e o
simbolismo antigos. Demonstrou que os caracteres dessa escrita derivaram da
divisão duodecimal do círculo e que, de fato, essa divisão ainda é usada hoje
no relógio e na bússola.
A influência da geometria egípcia e da magia caldaica foi
grandemente sentida pelos israelitas. Ao longo de toda a Bíblia, descrevem-se
em detalhe objetos e edifícios sagrados com medições precisas que ali se diz
terem sido dadas por Deus. A mais antiga dessas construções dimensionadas
canonicamente é a mitológica Arca de Noé, descrita da seguinte maneira:
"Faze para ti uma arca
de madeira alisada; farás nela uns pequenos repartimentos, e betumá-Ia-ás por
dentro e por fora. E eis aqui como a hás de fazer; ela terá trezentos côvados
de comprimento, cinquenta de largura e trinta de altura. Farás na arca uma
janela, e o teto que a há de cobrir será de um côvado; porás também nela uma porta
a um lado; e disporás um andar em baixo, um no meio e outro terceiro andar.”
Gênese 6: 14-16.
Na tradição cabalística, a Arca de Noé é dividida em três
andares, com 11 seções cada um, o que perfaz o número sagrado 33. A Arca
possui duas aberturas: a porta principal no andar mais baixo, por onde as vidas
animais passam para o plano da existência física, e uma janela pequena de um
côvado no alto da cabeça, por onde é solto o espírito, simbolizado pela pomba.
Muitos praticantes do conhecimento oculto comentaram esse
vaso sagrado. Filo, o Judeu, afirma que a Arca de Noé foi construída segundo o
padrão do corpo humano. Heinrich Cornelius Agrippa concorda. E escreve:
"Dado que o homem é a mais bela e a mais perfeita obra
de Deus, e a Sua imagem, e também o menor dos mundos, ele, portanto, por uma
composição mais perfeita, e uma harmonia doce, e uma dignidade mais sublime
contém e conserva em si todos os números, todas as medidas, todos os pesos,
todos os movimentos, todos os elementos, e todas as outras coisas que o
constituem; e nele, de fato, está a habilidade suprema (...) além disso, o
próprio Deus ensinou Noé a construir a Arca segundo a medida do corpo do homem
e Ele fez toda a estrutura do Mundo ser proporcional ao corpo do homem.
Portanto, alguns que escreveram sobre o microcosmo, ou sobre o homem, afirmam
que o corpo mede 6 pés, um pé 10 graus, cada grau 5 minutos; têm-se 60 graus,
que fazem 300 minutos, aos quais são comparados muitos côvados geométricos com
que Moisés descreve a Arca; pois, como o corpo de um homem tem 300 minutos de
comprimento, 50 de largura e 30 de altura, assim também a Arca era longa de 300
côvados, larga de 50 e alta de 30.”
Em The Canon, William Stirling relaciona as medidas da Arca
com o tamanho do planeta Terra e com os cânones da cronologia segundo a
história sagrada hebraica: "Se essa explicação for correta", escreve
Stirling, "devemos imaginar, pelas proporções da arca, a vasta figura de
um homem, à imagem e à semelhança de Deus, cujo corpo contém a medida do caminho
do sol na eclíptica, o circuito da Terra e as órbitas dos sete planetas".
Esses esquemas cosmológicos podem ser encontrados ao longo de
toda a arquitetura antiga, especialmente no Egito e na Babilônia. A Arca,
embora seja principalmente um barco em que um homem justo, sua família e seu
gado escaparam a um dilúvio que desabou sobre toda a terra, é na verdade uma
imagem cósmica do homem, o microcosmo que mais uma vez foi conformado ao padrão
dado por Deus. Aqueles que se ajustam ao esquema cósmico sobrevivem, os que não
se ajustam perecem.
Uma outra estrutura sagrada hebraica cujas dimensões, e por
conseguinte a geometria, foram precisamente delineadas foi o Tabernáculo. O
Tabernáculo era um santuário portátil utilizado pelo povo judeu durante as suas
peregrinações pelo Sinai. Sendo basicamente um templo móvel modelado segundo
protótipos egípcios, o Tabernáculo era colocado num pátio cuja geometria era a
do quadrado duplo, com 100 côvados de comprimento por 50 de largura. Esse pálio
era demarcado por uma cerca composta de estacas de 5 côvados de altura
plantadas no chão a intervalos de 5 côvados. As estacas eram ligadas por
cordões de linho duplo. Construía-se então toda a planta baixa do Tabernáculo
de acordo com uma grade quadrada modular de 5 côvados - método de esboço usado
no Egito, de onde os israelitas fugiram.
Dentro desse quaprado duplo, o Tabernáculo propriamente dito
era um quadrado triplo de 30 côvados de comprimento e 10 de largura. Suzs
paredes eram construídas de pranchas de madeira de 1 1/2 côvado de largura
e de 10 côvados de altura, agrupadas por fortes barras horizontais de madeira.
Toda a estrutura era coberta de peles costuradas em faixas de 30 côvados
de comprimento e 4 de largura. O Tabernáculo era colocado no pátio, orientado
para o oeste, mas sua entrada era orientada para o leste, de maneira que,
segundo Josefo, "quando o sol se erguesse, poderia pousar os seus
primeiros raios sobre ele".
Essa orientação, comum na arquitetura sagrada de todo o mundo,
assegura que a estrutura do santuário esteja integrada diretamente com os
fenômenos cósmicos. Isto é de importância fundamental para as épocas
astronomicameme definidas para a realização de rituais vitais. Como um
microcosmo, era necessário que o templo ou Tabernáculo refletisse diretamente
em suas dimensões, sua geometria e sua orientação as condições e a estrutura do
macrocosmo de que ele era a imagem e um meio de dirigir o acesso a ela. De
fato, Josefo afirma que “essa proporção das medidas do Tabernáculo era uma
imitação do sistema do mundo".
O interior do
Tabernáculo estava dividido em dois compartimentos, um esquema que foi copiado
mais tarde no Templo construído em Jerusalém sob as ordens do rei Salomão. O
compartimento externo, chamado de Lugar Santo, era um quadrado duplo de 20
côvados por 10, ao passo que o compartimento interno, o Santo dos Santos,
compreendia um quadrado simples. Como a altura do teto do Tabernáculo também fosse
de 10 côvados, o Santo dos Santos era assim um cubo perfeito.
No interior do Santo
dos Santos estava o objeto mais sagrado dos judeus, a Arca da Aliança. Como
outros objetos judaicos sagrados, suas medidas exatas foram registradas. A
Arca media 2 1/2 côvados de comprimento, metade do módulo usado no esboço do
Tabernáculo, e 1 1/2 côvado de largura e de altura. Stirling acreditava que
essas medidas tivessem significação cosmológica:
"Ela media 2 1/2
côvados de comprimento, ou 3 3/4 pés, ou 45 polegadas; sua largura e sua altura
mediam 1 1/2 côvado, ou 2 1/4 pés, ou 27 polegadas. Seu perímetro, era, então,
o número místico de 144 polegadas. Se a Arca fosse uma polegada mais grossa, o
que seria perfeitamente possível para uma caixa desse tamanho, seu conteúdo subiria
para 24.860 polegadas cúbicas, ou o número de milhas da circunferência da
Terra.”
Essa interpretação
fascinante, naturalmente, depende da antigüidade da polegada e da milha, um
problema espinhoso tornado de difícil solução pelas reivindicações
extravagantes que têm sido feitas na tentativa de uma interpretação dos
mistérios da Grande Pirâmide.
Outro objeto
geometricamente determinado que era guardado no Tabernáculo era a Mesa do
Pão da Proposição, modelada segundo um protótipo egípcio. Essa mesa sagrada
ficava do lado de fora do véu que dividia o Tabernáculo, e, por conseguinte,
não se situava no Santo dos Santos. Suas dimensões eram 2 1/2 côvados por 1 1/2
côvado e 1 côvado, uma razão de 5:3:2.
O Altar dos
Sacrifícios era o equivalente externo da Arca da Aliança. Ficava no centro do
mais externo dos dois quadrados que formavam o Tabernáculo. A base desse altar
era um quadrado de 5x5 côvados, o módulo modelo. Esse altar representava um dos
dois pólos do centro dos dois quadrados - cada um no seu próprio centro de
polaridade -, sendo que a combinação dos dois no pátio do Tabernáculo era a
unidade de opostos inerente ao Deus supremo. Esse dimensionamento e esse esboço
exatos de uma área sagrada propiciam-nos um raro lampejo do que existe de mais
canônico na geometria sagrada. Todo e qualquer objeto é definido precisa e exatamente
em termos de tamanho e situação, pois alterar qualquer coisa redundaria num
desastre.
A vida nacional dos
judeus alcançou seu ponto culminante durante o reinado de Salomão. Em 1004
a.C., o ato de coroação desse rei foi a ereção de um templo de adoração de
Jeová. Como outros artefatos hebraicos sagrados, o desenho do Templo foi
revelado divinamente ao pai de Salomão, o rei Davi:
"E
Davi deu a Salomão seu filho o desenho do pórtico, e o do Templo, e das
suas oficinas, e das suas salas, e dos seus aposentos interiores, e da
casa da propiciação. E o desenho de tudo que ele imaginara e das
repartições da casa do Senhor.”
1
Crônicas 28.
As dimensões do
Templo, bem como do Tabernáculo, antes dele, foram detalhadas exatamente:
"E
este foi o plano que lançou Salomão para construir a casa de Deus, sessenta
côvados de comprido pela primeira medida e de largura vinte côvados.”
2
Crônicas 3.
O Templo homologava
com um quadrado triplo o tamanho do Tabernáculo e suas paredes eram
revestidas de madeira recoberta de ouro. O interior compreendia um lugar
sagrado retangular, na forma de um quadrado duplo, e um Santo dos Santos
conformado em um quadrado simples. O interior possuía 20 côvados de altura, e
o Santo dos Santos formava novamente um cubo.
No centro mesmo do
Santo dos Santos ficava a Arca da Aliança, que ocupara anteriormente o
ponto central do Santo dos Santos do Tabernáculo. Em cada extremidade da
Arca havia um querubim dourado de asas abertas, de dez côvados de altura.
Esses dez côvados parecem ter sido o módulo de que derivaram as dimensões
do Tem plo e eram o dobro do tamanho do Tabernáculo portátil.
A entrada do Santo
dos Santos era fechada por uma porta de duas folhas, medindo cada uma
delas dois côvados de largura. A entrada para o Templo possuía 5 côvados
de largura e se abria de um pórtico que compreendia dois quadrados de
10x10 côvados. Era esse pórtico que suportava os dois pilares que
posteriormente assu miram grande significação no saber maçônico: Jachin e
Boaz.
Cada pilar possuía 12
côvados de circunferência e era coroado por um capitel em forma de lírio com 5
côvados de altura. Esse capitel repousava sobre um castão de 3 côvados de
altura que atra vessava 7 cadeias de romãs, 14 ao todo. O número místico
14 corresponde aos 14 quadrados de 10 côvados que constituem a planta baixa
do Templo; as 14 gerações tradicionais de São Mateus, de Abraão a Davi; e os 14
Passos Cristãos da Cruz. Novamente, o Templo incorporava vários esquemas
cosmológicos, condizendo com uma imagem do macrocosmo.
Esse primeiro Templo
de Jerusalém, o Templo de Salomão, foi destruído em 585 a.C., quando os
babilônios tomaram a cidade e expatriaram a maior parte da população como
escravos. Quando o longo cativeiro dos judeus na Babilônia chegou ao fim, os
cativos que retomavam encontraram o Templo demolido sobre o chão. O Livro de
Esdras dá-nos o seguinte relato:
"No
primeiro ano em que o rei Ciro reinou sobre o país da Babilônia, Ciro, o Rei,
ordenou reerguer esta casa. E os vasos sagrados de ouro e prata, que
Nabucodonosor tinha levado da casa de Jerusalém (...) Ciro, o Rei, os trouxe
do templo da Babilônia e eles foram entregues a Zorobabel e a Sanabassarus, o
governador (...) então o mesmo Sanabassarus deitou as fundações da Casa do
Senhor em Jerusalém (...) no primeiro ano de Ciro, o rei Ciro ordenou que a
casa do Senhor em Jerusalém fosse reconstruída, onde eles deviam sacrificar em
fogo contínuo. Cuja altura deveria ter sessenta côvados, e a largura sessenta
côvados, com três fileiras de pedras esculpidas, e uma fileira de madeira nova
daquele país (... ).”
Assim, o segundo
templo, construído sob ordens expressas do conquistador persa, era uma
estrutura quadrada com lados de 60 côvados. Altura é um termo antigo às vezes
usado para significar comprimento, mas é possível que o templo tivesse a forma
de um zigurate. Fosse assim, ele devia apresentar quatro estágios
("fileiras" de pedra e madeira talhada). Seja qual for a forma
assumida pelo templo, suas dimensões estavam baseadas no velho templo, pois seu
comprimento era de 60 côvados, excluindo-se o pórtico de Boaz e Jachin.
Pouca coisa mais foi
registrada a respeito desse templo, exceto que todos os objetos sagrados que foram
levados à Babilônia e instalados no templo principal retomaram e foram
novamente utilizados nos serviços judaicos. A forma do segundo templo, um
quadrado, não era característica dos judeus e deve ter origem persa. De acordo
com o Talmude, o primeiro templo foi construído por meios sobrenaturais e,
segundo a Bíblia, por trabalhadores fenícios, sob a direção de Hiram Abiff. Se
o segundo templo foi de execução persa, sua variação em desenho pode ser
responsável pela rapidez de sua ereção - durante o primeiro ano da libertação.
Todavia, como o primeiro templo, estava fadado a ser demolido por
invasores.
No Primeiro Livro dos
Macabeus está escrito. que "quando eles viram o santuário deserto e o
altar profanado e as portas queimadas e os arbustos crescidos nos átrios como
numa floresta (...) rasgaram suas vestes e fizeram grande pranto e puseram
cinzas sobre suas cabeças". Todavia, as técnicas e o conhecimento
envolvidos na reconstrução do Templo haviam sido perdidos e, em vez de o
reedificarem, Judas Macabeu e seus homens demoliram as ruínas. "Eles
acharam melhor demoli-Io, temendo não viesse ele ser-Ihes um motivo de opróbrio,
por causa de o terem contaminado os gentios, assim eles o demoliram. E
puseram as suas pedras no monte do Templo num lugar propício, esperando. que
surgisse um profeta que lhes mostrasse o que fazer com elas.”
Isto mostra que a canhecimento
da geometria sagrada exigida para erigir um novo edifício sagrado faltava ao
piedoso mas profano bando militar de Judas. Era necessário um profeta que fosse
dotado do conhecimento esotérico apropriado, mas ele não existia. Um templo
substitutivo não foi construído até a época de Herodes, que fez erigir uma
réplica exata do santuário de Salomão. Apenas uma parede do Templo de Herodes
está de pé, até hoje, na forma do famoso "Muro das Lamentações"'. O
templo em si mesmo foi demolido novamente, desta vez pelos romanos na sua
guerra colonial contra os judeus no ano 70 d.C.
6. Grécia
Antiga
"Com
a harmonia, com a celestial harmonia
Teve
início essa estrutura universal;
E,
de harmonia em harmonia,
Percorreu
todas as notas da pauta,
Culminando
o diapasão no homem ao fina!.”
Dryden,
A Song for Sr. Cecilia's Day.
Os gregos antigos
foram notáveis por sua abordagem pioneira e experimental do mundo.
Numerosos filósofos elabararam teorias que outros discutiram com argumentas
ponderados e experimentos práticos. Nesse ambiente estonteante, uma descoberta
importante que exerceu grande influência sabre a geometria sagrada foi feita
por Pitágoras no século VI a.C. Ele descabriu que as cordas percutidas em um
instrumento soavam em harmonia quando as suas extensões estavam relacionadas a
uma outra por determinados números inteiros.
Pitágoras fizera a
descoberta radicalmente importante de que os tons podem ser medidos em
termos de espaço. Ele descobriu que as consonâncias musicais podem ser
expressas em razões de números inteiros. Por exemplo, se duas cordas vibram sob
as mesmas condições, tendo uma a metade da extensão da outra, a afinação da
corda menor será um diapasan (uma oitava) acima da maior. Se as cordas possuírem
uma razão de extensão 2:3, a diferença de afinação. será um diapente (uma
quinta) e, se a razão de extensão for 3:4, a diferença será um diatessaron (uma
quarta). Essas consonâncias pitagóricas são, assim, expressas em termos da
progressão simples 1:2:3:4, que contém, além do diapasan, da diatessaron e
de diapente, a oitava-e-quinta, 1:2:3:, e duas oitavas, 1:2:4.
Quando este esquema
foi redivulgado no século XVI da era cristã, ele constituiu a base dos sistemas
harmônicos da arquitetura sagrada da Renascença. A descoberta de Pitágoras foi
considerada em termos de uma revelação divina da harmonia universal. Todo o
universo podia então ser explicado em termos matemáticos. A fim de conseguir
mestria sobre esse universo, afirmavam os pitagóricos, o homem devia
descobrir os números que estão ocultos em todas as coisas. A revitalização
dessa doutrina vinte e dois séculos depois foi responsável pelo desenvolvimento
explosivo da ciência que reformulou o mundo em sua imagem moderna.
Os pitagóricos
afirmaram que os números eram unidades independentes que possuíam determinadas
dimensões espaciais indivisíveis e eternas. Todavia, a despeito dessa teoria,
eles foram capazes de, na prática, perceber que as diagonais dos quadrados, por
exemplo, não são mensuráveis em unidades inteiras. Pitágoras chamava esses
números de "incomensuráveis". Mais tarde, números como V3 foram
chamados de "irracionais", isto é, que não podem ser expressos em
medida. De qualquer maneira, a idéia pitagórica das unidades finitas foi
rapidamente criticada por Zenão, que, por meio do seu famoso paradoxo, desacreditou
a teoria.
Pitágoras afirmava
que esses números e suas proporções eram fundamentais para a estrutura de todo
o mundo. O cubo era a perfeição culminante, pois é impossível, em termos de
geometria clássica, ir além da terceira dimensão de comprimento, de largura e
de altura.
Levando adiante o
saber pitagórico sobre o número, Platão (428-347 a.C.), em seu Timeu, declarou
que a harmonia cósmica está contida em determinados números formados nos cubos
e nos quadrados de proporção dupla e tripla que começam na unidade. Eles são
criados por duas progressões geométricas - 1, 2, 4, 8 e 1, 3, 9, 27. Tradicionalmente
representados com a letra grega lambda, eles impregnam a tradição geométrica
européia desde a Grécia até a era moderna. Para Platão, a harmonia do universo
estava expressa em sete números (o próprio 7 é um número místico): 1, 2, 3, 4,
8, 9, 27 - figuras que abarcam os mistérios do macrocosmo e do microcosmo, números
adequados mais que todos os outros para incorporação à arquitetura sagrada.
Na sua prescrição
para a fundação de uma nova cidade, Platão afirmou que todos os detalhes
exigiam a atenção mais dedicada. Declarou que os templos deviam ser erigidos ao
redor de um mercado e por toda a cidade em pontos elevados. A natureza
geométrica do plano da cidade era dada por reconhecida. Seu desenho geomântico
devia ser regulamentado por uma Comissão Urbana dotada de poderes para proibir
quaisquer alterações não autorizadas. Acreditava-se que esse desenho
geomântico que governava a cidade devia ser essencial à felicidade dos
habitantes. Platão acreditava que o povo jamais conheceria a felicidade se os
desenhistas de suas cidades fossem artistas que não tomassem o divino como seu
padrão.
Esse padrão divino,
tal como apresentado na República de Platão, era um esquema cosmológico que
representa o microcosmo. Até mesmo o número de habitantes da cidade era ideal -
5.040 moradores, que ocupavam o mesmo número de iates. Esse número é quase
universalmente divisível, sendo derivado da multiplicação sucessiva dos números
de 1 a 7, donde ser divisível por todos os números de 1 a 10, bem como por 12.
Todo o território que rodeasse a acrópole devia ser dividido em 12 partes, mas
a igualdade deveria ser assegurada pela condição engenhosa de que os
alotamentos de terra ruim deviam ser maiores do que os alotamentos de terra boa
- uma tarefa difícil, se não impossível. A República era um microcosmo
alegórico em todo sentido. Todos os seus atributos geométricos e numerológicos
refletem o ideal divino, cuja consumação, se conseguida, uniria o homem ao
universo - o que sempre foi o objetivo final dos mágicos e dos alquimistas.
O geômetra mais
famoso de todos os tempos, Euclides, era, naturalmente, grego. Sua obra,
conhecida como Elementos, tornou-se o manual da geometria até este século.
Nela; por meio de teoremas e provas, as relações básicas da geometria foram
definidas de maneira racional. Sua geometria era puramente teórica e pode representar
a primeira vez na história que a teoria foi estudada em si mesma e não como
parte integrante de uma praxis. Em Euclides, a geometria prática está
diretamente relacionada às razões do número inteiro que eliminam qualquer
necessidade de medir ângulos. Assim, até a Renascença, quando número e medição
angular se tornaram importantes para a artilharia, as razões do número inteiro
eram invariavelmente empregadas na arquitetura sagrada.
No seu livro A
History of Architecture in All Countries, James Fergusson escreve:
"O sistema da
proporção definida que os gregos empregavam no desenho dos seus templos foi
outra causa do efeito que eles produzem sobre as mentes incultas. Para eles não
só a altura deveria' ser igual à largura, ou comprimento duas vezes a largura -
mas toda e qualquer parte devia ser proporcional a todas as partes com que ela
se relacionava, em alguma razão tal como 1 para 6, 2 para 7, 3 para 8, 4 para
9, ou 5 para 10, etc. A medida que o esquema avança, esses números tornam-se
consideravelmente altos. Nesse caso, eles revertem para alguma razão simples,
tal como 4 para 5, 5 para 6, 6 para 7, e assim por diante.”
Essa proporção não
está tão evidente, em nenhum outro lugar, como no Partenon, em Atenas. Esse
magnificente templo pagão, agora em ruínas, foi construído como substituto de
um templo menor de Atenas que fora destruído pelos persas em 480 a.C. Por ter
sido construído sobre as fundações de. um templo mais antigo, que por sua vez
também substituíra uma Sala do Trono micênica, o Partenon foi projetado mais
como medidas micênicas do que com o usual pé grego. As dimensões principais
foram tão bem escolhidas que correspondiam a números redondos em pés tanto
gregos quanto micênicos, uma tarefa não de todo difícil, já que as medidas estão
relacionadas na razão 10:9. Essa relação simples é freqüentemente encontradiça
em medidas relacionadas, tais como os pés galeses, ingleses e saxões.
A geometria do
Partenon foi tão bem planejada, que incorporava todas as medidas
significativas. Suas dimensões foram meticulosamente registradas por Francis
Cranmer Penrose, um arquiteto inglês que mediu o templo com uma precisão que
considera até mesmo um milésimo do pé inglês. Penrose determinou que o Partenon
não foi construído com linhas retas, mas utilizou curvas matemáticas sutis na
sua estrutura. Assim, o Partenon representa outra ordem de geometria, algo
quase fora do comum. Penrose determinou que existem similaridades essenciais
entre as estruturas geométricas do Partenon e da Grande Pirâmide. As elevações
das fachadas do Partenon foram determinadas pela Seção Dourada e os lados foram
baseados no fator phi. O Professor Stecchini calculou que os desvios mínimos
encontrados nas bases tanto do Partenon quanto da Grande Pirâmide foram
cometidos deliberadamente e não eram resultado de pequenos erros de
cálculo. Na sua opinião, a relação entre (I) e phi na extremidade e no lado do
Partenon é um paralelo daquela que existe entre a face norte da Pirâmide (I) e
o lado oeste phi.
A largura das
fachadas do Partenon era tal, que indicava um segundo de um grau no equador.
Assim, as partes individuais da estrutura, todas comensuravelmente
proporcionais em relação à geometria subjacente a todo o edifício, eram
proporcionais às dimensões da própria Terra. A harmonia divina, assim
engendrada, integra o edifício com o cosmos. Ele se torna parte integrante da
harmonia global do mundo e é, dessa maneira, um receptáculo perfeito para
adoração. A necessidade tríplice de um templo funcional - orientação,
geometria e medida - estão presentes no Partenon e em qualquer outro edifício
verdadeiramente sagrado plantado em qualquer canto da Terra. Esse grau de
integração não é conseguido por meio de nenhum outro método.
A geometria impregnou
toda a esfera da vida grega. A conexão íntima entre a forma geométrica e a
história sagrada pode ser vista no problema supostamente insolúvel da
duplicação do cubo. Os délios, que, na época de Platão, estavam sendo vitimados
por uma peste, consultaram o oráculo para cons,eguirem um meio de dela se
libertarem. O oráculo ordenou-Ihes duplicar um dos seus altares cúbicos.
Dirigiram-se então aos geômetras da Academia e lhes pediram resolvessem o
problema como um assunto de urgência nacional. Na verdade, trata-se de um
problema insolúvel pelos métodos clássicos da geometria e, por conseguinte,
está excluído da categoria da geometria sagrada. É um equivalente em termos
geométricos do extrair a raiz cúbica de dois, que não pode ser expressa em
termos de números inteiros nem em termos de raízes quadradas de números
inteiros. O fato de esse problema ter sido proposto pelo oráculo indica a
seriedade com que a geometria estava investida na Grécia. A observância correta
da forma geométrica na arquitetura sagrada era um ato mágico que. poderia
livrar um país de uma dificuldade.
A duplicação do cubo
foi mencionada num drama teatral grego, agora perdido. O geógrafo Eratóstenes,
que utilizou esse conhecimento geométrico para medir o tamanho da Terra, relata
numa carta escrita ao rei Ptolomeu IIl do Egito que um dos poetas trágicos
antigos se refere ao problema. Na peça, ele apresenta o rei Minos sobre o palco
erigindo uma tumba para seu filho Glauco, e então, percebendo que a estrutura
era muito insignificante para um mausoléu real, ordenou "duplicá-Ia mas
preservar-lhe a forma cúbica".
Esses dois exemplos
enfatizam a importância do volume na arquitetura sagrada egipto-grega. Como as
dimensões internas do cofre colocado dentro da Grande Pirâmide, a capacidade
das estruturas sagradas merecia consideração primária. Exemplos posteriores da
Europa medieval e renascentista também mostram que a capacidade era o fator
mais determinante. As dimensões internas eram sempre estipuladas no desenho das
igrejas e das capelas, ao passo que geometria sagrada elevacional era aplicada
às elevações exteriores. O "problema délio", como ficou conhecido, da
duplicação do cubo foi reduzido por Hipócrates de Chios a uma questão de
geometria plana, isto é, à descoberta de duas proporcionais entre duas linhas
retas, a maior das quais deve ser o dobro da menor. Esse foi mais um dos
problemas teóricos pelos quais Euclides e seus seguidores se tomaram conhecidos.
Ele levou à descoberta das seções cônicas.
Já neste período tão
primitivo, esse interesse literalmente acadêmico pela geometria dividia o
assunto em duas disciplinas distintas, a prática e a matemática. Ao passo que
havia (e ainda há) uma grande coincidência entre as geometrias sagrada e
matemática, as raízes do cisma podem ser encontradas nos esforços feitos pelos filósofos
gregos na tentativa de resolver os problemas geométricos do oráculo.
A beleza da arte
grega foi o resultado prático das meditações dos filósofos. Naqueles
tempos, quando a reverência pagã antiga para com o mundo ainda não havia
sido superada pela espoliação a todo custo que caracteriza a civilização
industrial, todo objeto que passasse pelas mãos dos artesãos continha
propriedades sagradas. O artesão, diferentemente da sua contrapartida moderna
da linha de produção, estava consciente da natureza sagrada dos materiais com
que trabalhava e da sua responsabilidade como fiduciário do material que manipulava.
Porque toda a Terra
era sagrada, os materiais também eram sagrados e, assim, a modelagem era um ato
de adoração. Era imperativo que o artesão trabalhasse com o melhor da sua
habilidade e em concordância com os materiais de que dispunha; assim, a aplicação
da geometria sagrada era absolutamente natural. Os vasos gregos requintadamente
belos foram analisados por geômetras modernos tais como Caskey e Hambidge, que
descobriram que eles foram desenhados de acordo com construções complexas mas
harmoniosas de geometria de Seção Dourada. Fazer vasos e utensílios sagrados
de acordo com a geometria sagrada asseguraria a sua função correta não só nos
arredores do templo, cuja geometria eles ecoavam, mas também no contexto
secular. É só nos tempos modernos que a geometria sagrada foi relegada,
primeiramente à esfera estreita do desenho de edifícios sagrados, e depois
completamente abolida em função de objetivos prático.
7. Vitrúvio
"A
necessidade do arquiteto é criar aquele uníssono de partes e detalhes que nas
melhores edificações de todos os tempos remontou miraculosamente os processos
imaginativos a quantidades matemáticas e a contextos geométricos.”
Erich
Mendelsohn (1887-1953)
Marcus Vitruvius
Pollo, comumente conhecido como Vitruvius [Vitrúvio], foi um arquiteto e
engenheiro romano que trabalhou no primeiro século antes da nossa era. Foi
autor de um tratado teórico e técnico detalhado que sobrevive como a mais
antiga e a mais influente de todas as obras sobre a arquitetura.
A posição de Vitrúvio
como o arquiteto mais influente de todos os tempos é atestada pelo seguinte
fato. Durante séculos, as instruções detalhadas forneci das nos Dez Livros de
Arquitetura foram seguidas mais ou menos fielmente em toda a extensão de tempo
coberta pelo Império Romano. Após a queda desse Império, as formas bárbaras de
arquitetura foram introduzidas e as instruções canônicas de Vitrúvio foram
largamente ignoradas ou deturpadas.
Após quase um milênio
de obscuridade, a redescoberta de suas obras anunciou a renascença na arquitetura,
quando seu livro tornou-se repentinamente a autoridade principal consultada
pelos arquitetos. Seus preceitos foram a partir de então aceitos como sacrossantos.
Na verdade, os maiores arquitetos da Renascença na Itália - Miguel Ângelo,
Bramante, Vignola e Palladio - foram todos eles estudiosos ardorosos da obra de
Vitrúvio e cada uma de todas as suas obras-primas deriva diretamente dos
sistemas proporcionais enumerados por Vitrúvio.
Os Dez Livros
escritos por Vitrúvio são um cômputo completo da arquitetura, desde a educação
inicial do arquiteto, passando pelos princípios fundamentais da arte, da
localização geomânticados templos e das cidades, das casas para moradia, dos
materiais e das formas de arquitetura, até a pintura, a maquinaria e as artes
militares. Segundo Vitrúvio, a arquitetura depende da ordem, do arranjo, dll
curritmia, da simetria, da propriedade e da economia. A ordem proporciona a
medida exata das partes de uma obra consideradas Isoladamente e da concordância
simétrica das proporções de todo o edifício. O arranjo envolve a colocação das
coisas em sua ordem própria, sendo as suas formas de expressão a planta baixa,
a elevação e a perspectiva. Inclui a utilização sucessiva apropriada dos
compassos e da régua, o artifício fundamental do geômetra.
A eurritmia consiste
na beleza e na conveniência no ajustamento das partes. Vitrúvio afirma que
quando se consegue a comodulação perfeita (a ligação de todos os elementos
arquitetônicos com o todo por meio de um sistema de proporção), consegue-se
também a eurritmia. Isso nem sempre era possível por razões técnicas, mas a
simetria dinâmica, um conceito encontrado nos escritos de Platão, provou ser
freqüentemente um substituto aceitável. Na simetria dinâmica, embora os
elementos lineares não sejam comensuráveis, as superfícies construídas sobre
eles podem ser comensuráveis, encadeadas por meio de uma proporção racional.
A simetria é a
concordância justa entre as partes da própria obra e a relação entre os
diferentes elementos e todo o esquema geral de acordo com uma determinada parte
escolhida como padrão. Assim, no corpo humano, Vitrúvio demonstra a harmonia
simétrica que existe entre o antebraço, o pé, a palma, o dedo e outras partes
menores. Compara essas partes às partes de um edifício, continuando a antiga
tradição do edifício sagrado visto em termos do corpo de um homem e, assim, em
termos do microcosmo.
Vitrúvio define a
propriedade como aquela perfeição de estilo que surge quando uma obra é
construída peremptoriamente segundo princípios canônicos. A propriedade emana
da prescrição, dos métodos aceitos para a construção dos templos dos deuses.
Vitrúvio deve ser agradecido pela preservação dessas formas prescritas:
pelos edifícios em campo raso, abertos para o céu, em honra de Júpiter, do
Raio, dos Céus, do Sol ou da Lua; para Minerva, Marte e Hércules, a Ordem
Dórica; para Vênus, Prosérpina, Flora, para a Água da Fonte e para as Ninfas, a
Ordem Coríntia; e para Juno, Diana, Baco e outros deuses, a Ordem Jônica. A
propriedade, todavia, também podia ser conseguida pela ereção de templos em
terrenos saudáveis onde existissem fontes convenientes. Os santuários deviam
ser construídos nessas fontes e este era um dos princípios fundamentais para
templo que sublinhavam o que agora é conhecido como geomancia. A propriedade
também era conseguida nos edifícios pela orientação apropriada, de maneira que
a luz pudesse ser utilizada para o benefício supremo de todos.

A economia, O último
princípio de Vitrúvio, é auto-explicativa. Todas as suas máximas ecoam o
funcionalismo realístico do mundo antigo, concedendo todas as condições antes
de se decidir sobre a forma de um edifício enquanto sob o controle global da
geometria sagrada. Assim. conseguia-se uma síntese de natural e artificial, terreno
e celeste, um equilíbrio a que o movimento ecológico moderno está tentando
chegar com muito esforço. Vitrúvio, embebido na harmonia geomântica antiga
entre o homem e o mundo, viu o desenho do edifício em termos do corpo de um
homem. Os desenhos bastante conhecidos que mostram o corpo de um homem
superposto a uma geometria são conhecidos até hoje como o Homem Vitruviano.
Todavia, nem todo arquiteto vitruviano trabalha com as proporções do corpo de
um homem. Elas estão reservadas aos templos. A estrutura do teatro e da cidade,
construções com funções materialmente diferentes, está relacionada à forma
conceptual do mundo e é mais radial do que linear.
A construção do
teatro - pela primeira vez dada por escrito por Vitrúvio, mas certamente de uma
antigüidade maior - demonstra a sua natureza como um microcosmo do mundo. Essa
idéia foi retomada na Renascença e cultuada no "Todo o mundo é um palco
(...)" de Shakespeare, e, na verdade, fisicamente, nesse teatro tão
adequadamente chamado Globo. A estrutura do teatro prescrita por Vitrúvio era
a seguinte: "Tendo fixado o centro principal, desenhar uma linha de
circunferência equivalente ao perímetro da base e nela inscrever quatro
triângulos eqüiláteros, a distâncias iguais e tocando a fronteira do círculo,
como fazem os astrólogos na figura dos doze signos do zodíaco, quando eles
estão procedendo aos cálculos da harmonia musical das estrelas". A partir
desse esboço de ad triangulum, as várias partes essenciais do teatro eram proporcionais.
Mesmo o cenário era baseado no triângulo, em "peças triangulares de
maquinaria que giram, cada uma delas com três faces decoradas (...) Há três
espécies de cenas, uma chamada trágica, a segunda cômica e a terceira satírica
(...)". Até mesmo os eventos representados nesse teatro estavam divididos
em três.
Todavia, este não foi
o único tipo de teatro descrito por Vitrúvio. O teatro grego baseava-se mais
em três quadrados do que em quatro triângulos, uma geometria duodécupla
alterada que propiciava uma distribuição alternativa dos elementos que
guardava a natureza diferente dos dramas ali representados.
O pronunciamento de
Vitrúvio sobre a geometria grega talvez seja a mais expressiva das suas
exposições sobre a função da geometria sagrada e sobre sua posição na corrente
principal do pensamento hermético:
"As diversas
partes que constituem um templo devem estar sujeitas às leis da simetria; os
princípios dessa simetria devem ser familiares a todos os que professam a ciência
da arquitetura. (...) A proporção é a comensuração das várias partes constituintes
com o todo e o fundamento da existência da simetria. Pois nenhum edifício pode
possuir os atributos da composição em que a simetria e a proporção não sejam
observadas; e aí nem existe a conformação perfeita das partes que se pode observar
num ser humano bem formado (...) portanto, a estrutura humana parece ter sido
formada com tal propriedade, que os muitos membros são proporcionais ao todo.”
A obra de Vitrúvio
sobre a arquitetura foi uma tentativa de compilar um compêndio completo do
conhecimento aplicado. Com esse objetivo, ele expôs não só a geometria sagrada
das partes dos edifícios e a sua relação com edifícios inteiros, mas também o
planejamento de cidades. Após descrever os atributos para o sítio de uma
cidade, enumera os pontos que a cidade ideal deve conter. Naturalmente, sua
cidade baseava-se numa geometria rigorosa, mas, sendo um esquema ideal, nunca
foi construída durante a duração do Impé rio Romano. Mil e quinhentos
anos deveriam passar antes que essa cidade planejada fosse iniciada.
A Cidade Vitruviana,
como é conhecida, foi planejada sobre uma forma octogonal. Esse desenho opõe-se
ao modelo das colônias romanas então predominante, que era um retângulo
quartado. A cidade octogonal dividia-se de acordo com os "ventos".
Vitrúvio leva muito a sério o conceito dos oito ventos, embora possa tê-Io
feito para ocultar uma doutrina mais esotérica da geometria. Tradicionalmente,
as oito direções do compasso eram denominadas segundo um "vento".
Esse sistema ainda estava em uso na Itália no século XVII da nossa era em
instrumentos de agrimensura. Um circunferentor feito em Modena em 1686, que
está agora no Museu da Ciência, em Londres, exibe um mostrador de bronze sobre
o qual foram gravados os nomes de 32 ventos, um desenvolvimento daqueles
usados na época de Vitrúvio.
A fim de dividir o
círculo para determinar as direções dos oito ventos, Vitrúvio utiliza um método
clássico da geometria. Como o Manasara Shilpa Shastra hindu, o omphalos
original de que derivou a geometria é marcado por um gnômon. Esse ponto central
era marcado em Atenas pela Torre dos Ventos octogonal. Vitrúvio fornece
instruções precisas:
"Por volta da
quinta hora da manhã, tomar a extremidade da sombra projetada por esse gnômon e
marcá-Ia com um ponto. Depois, abrindo-se o compasso para o ponto que marca a
extensão da sombra do gnômon, descrever um círculo a partir do centro. À
tarde, olhar a sombra do gnômon à medida que ela aumenta e, quando ela tocar a
circunferência do círculo e a sombra for igual em extensão àquela da manhã,
marcá-Ia com um ponto. A partir desses dois pontos descrever com seus compassos
arcos interseccionantes e, através de sna intersecção e o centro, traçar uma
linha em direção à circunferência do círculo; eis o diâmetro que deve separar
os quartos do norte e do sul. Depois, utilizando-se a décima-sexta parte da
circunferência do círculo como diâmetro, descrever um círculo (...) a partir
dos quatro pontos assim descritos, traçar linhas que interseccionam a circunferência
de um lado a outro. Assim, teremos uma oitava parte da circunferência para
Auster e outra para Septentrio. O resto da circunferência é então dividido em
três partes iguais em cada lado e temos então desenhada uma figura igualmente
partilhada entre os oito ventos.”
A geometria aqui
estava diretamente relacionada às condições astronômicas do dia escolhido para
a fundação da cidade. Como o dia fora escolhido de acordo com aspectos
astrológicos auspiciosos, o esboço estava por conseguinte diretamente
relacionado àqueles aspectos, reproduzindo a velha máxima do "acima, como
abaixo". Como a República de Platão, a Cidade Vitruviana era mais um
ideal cósmico do que uma realidade concreta sobre a terra. Como em toda
arquitetura mística anterior ao nosso século, o aspecto numinoso simbólico era
considerado a forma verdadeira, ao passo que a manifestação material era vista
como uma simples sombra da sua contrapartida espiritual. A geometria sagrada
possibilitava ao arquiteto a criação de um instrumento funcional em que poderiam
ser utilizados ao máximo muitos atributos da forma esotérica aos níveis psicológico
e espiritual. Freqüentemente, as exigências da construção obrigavam o resultado
final a sair fora desse ideal, mas ocasionalmente todos os fatores estavam
presentes e surgia então uma obra-prima. Tais obras-primas seriam os modelos
da mística da Renascença mil e quinhentos anos depois.
8. Os
Comacinos e a Geometria Sagrada Medieval
Through
good gemetry,
Thys
onest craft of good masonry
Was
ordeynt and made in thys manère,
Y-cownterfetyd
of thys clerkys y-fere;
At
these lordys prayers they cownterfetyd gemetry,
And
gaf hyt the name of masonry
Far
the most oneste craft of alIe.
Ars
Gemetrie (século XIV).
Quando o Império
Romano Ocidental sucumbiu aos ataques violentos de ondas sucessivas de bárbaros
migrantes, a ereção de obras arquitetônicas em larga escala foi interrompida.
Não havia mais nenhuma estrutura político-econômica para planejar ou pagar
grandes obras cívicas ou eclesiásticas e, por conseguinte; as habilidades bastante
desenvolvidas que existiam antes foram-se reduzindo gradualmente. Embora o
conhecimento vitruviano sobrevivesse intacto nos reinos de Constantinopla,
ele foi totalmente extirpado do Ocidente, que tomou uma direção diferente.
Com a influência
bárbara, as formas clássicas puras de Roma transformaram-se gradualmente numa
arquitetura radicalmente diferente - a medieval. O Colégio de Arquitetos de
Roma, cuidadosamente controlado, fora dispersado e idéias e influências
individuais foram assimiladas. Com a perda de uma autoridade central,
grupos autônomos de homens com conhecimento arquitetônico reuniram-se
numa espécie de federação de pedreiros artesãos - os antecessores dos
franco-maçons medievais que tiveram controle exclusivo sobre a construção das
catedrais posteriores. De acordo com a antiga tradição maçônica, membros
refugiados do dispersado Colégio Romano de Arquitetos fugiram para Comacina,
uma ilha fortificada do lago de Como, na Itália, onde resistiram durante vinte
anos às incursões dos lombardos que então estavam invadindo o país. Quando
finalmente foram subjugados, os reis lombardos tomaram os ar quitetos a
seu serviço para assessorarem a reconstrução. A partir desse centro,
afirma a lenda, os maçons, chamados de comacinos por causa do seu refúgio
fortificado, espalharam-se por toda a Europa ocidental e setentrional,
construindo igrejas, castelos e obras cívicas para os governantes dos estados
nacionais nascentes que se seguiram ao Império Romano.
Os comacinos estavam
certamente a serviço de Rotharis, um rei lombardo, que a 22 de novembro de 643
fez publicar um edito relativo, entre outras coisas, aos comacinos. O título do
Artigo 143 desse edito era Dos Mestres Comacinos e seus Colégios. O Artigo 144
dispõe: "Se uma pessoa qualquer empregar ou contratar um ou mais mestres
comacinos para desenharem uma obra (...) e acontecer de um comacino ser morto,
o proprietário da casa não será considerado culpado". Pode-se inferir daí
que os comacinos constituíam um poderoso corpo contra o qual o rei achava que
seus súditos deveriam ser protegidos. Joseph Fort Newton, em seu livro maçônico
The Master Builders, fala de uma pedra gravada no ano 712 que, mostrava que a
guilda dos comacinos estava organizada em três classes: discipuli e magistri
sob as ordens de um gastaldo, um Grão-mestre.
Como qualquer outro
grupo de técnicos dotados de habilidades apreendidas, os comacinos ocupavam uma
posição de poder e de influência. Na Europa Setentrional, onde estavam
estampados todos os sinais da prática arquitetônica romana, era solicitada
a prática comacina. Como os magos, os adivinhos, os astrólogos e os geomantes
que cercavam a corte, nenhum rei respeitado da Idade das Trevas podia ficar sem
seu séquito de comacinos. Durante seu reinado, eles construíam seus palácios,
suas capelas e suas igrejas; por ocasião de sua morte, impressionantes
mausoléus como os de Teodorico em Ravena, na Itália, ou o de Etevaldo em
Repton, na Inglaterra. Essas igrejas e esses mausoléus eram o repositório do
conhecimento dos comacinos sobre a geometria sagrada.
O venerável Bede, em
suas Lives ot the Abbots, conta-nos que, no ano 674, o rei Ecgfrith da
Nortúmbria decidiu construir um mosteiro para Benedito, o homem santo local.
Para tanto, doou 8.400 acres do seu próprio estado em Wearmouth. "Após não
mais de um ano da fundação do mosteiro, Benedito cruzou o mar e veio a
Gaul e procurou, encontrou e levou de volta com ele os maçons que deveriam
erigir para ele uma igreja no estilo romano, de que ele sempre gostara".
As igrejas de pedra
da Nortúmbria e as obras-primas erigidas após a renascença instigadas pelo
imperador Carlos Magno apresentam um desenvolvimento gradual em complexidade e
sofisticação. Um ponto de referência capital neste processo é a Capela Palatina
de Aachen (Aix-Ia-Chapelle). Uma igreja redonda, baseada no octograma, a capela
apresenta um retorno das influências do Império Oriental, que naquela época
ainda florescia ao redor de ConstantinopIa. Todavia, igrejas contemporâneas na
Inglaterra apresentam uma base geométrica mais simples. A análise de muitas
igrejas saxônicas de Essex demonstrou que retângulos de raiz 3, 4, 5, 6 e mesmo
7 eram gerados para as plantas baixas por meio de um método simples de
construção. As igrejas de Inworth, Strethall, Chickney, Hadstock, Little Bardfield,
Fobbing, Corringham e White Roding possuem razões comprimento: largura que se
aproximam da raiz 3. A proporção geométrica, incomum em tempos posteriores, era
o resultado do esboço dos fossos da fundação por meio de uma corda, justamente
como a prática egípcia antiga.
A orientação da linha
do centro era determinada pela observação direta do nascer-do-sol no dia do
padroeiro. O maçom mestre demarcava a largura pré-estabelecida da igreja ao sul
da linha do centro. Um assistente caminhava então para a extremidade norte da
mesma linha, arreando a corda. Depois, traçava-se um quadrado e, do quadrado,
uma diagonal. A diagonal era esboçada como o comprimento, fazendo-se um
retângulo de raiz 2. A diagonal desse retângulo era então tomada com a corda e
dessa maneira se obtinha um retângulo de raiz 3. O retângulo da planta baixa da
nave podia então ser completado, usando-se a corda para medir a igualdade das
diagonais.
Esse método
parece-nos ser peculiarmente saxão, pois as igrejas normandas posteriores da
área foram construídas geralmente com base no quadrado duplo ad quadratum. Os
maçons de Carlos Magno utilizaram os métodos adotados posteriormente pelos
normandos e esses métodos "bárbaros" de geometria sagrada foram
relegados à arena da arquitetura secular vernacular. A arquitetura de CarIos
Magno e as suas imitações foram uma revitalização consciente da corrente
principal dos métodos romanos, utilizados na famosa igreja redonda de San
Vitale em Ravena, na Itália. Essa estrutura microcósmica, cujo objetivo foi
demonstrado aos cognoscenti por um ladrilho feito na forma de um labirinto,
foi construída no século VI por maçons de Constantinopla que haviam absorvido a
geometria asiática e alguns dos seus métodos de construção. Todavia, foi só
muitos séculos depois que um influxo de idéias árabes foi combinado com uma
consciência romana desenvolvida para criar as grandes catedrais do período
gótico.
A infusão de idéias
emprestadas do mundo islâmico marcou um desenvolvimento importante na
história da arquitetura sagrada ocidental. As idéias e a práticas geométricas
do mundo clássico tardio foram aprendidas pelos árabes quando eles
conquistaram cidades universitárias de importância vital como Alexandria
muitos séculos antes. Textos como os Elementos de Geometria de Euclides foram
traduzidos para o árabe e aplicados à nova arquitetura sagrada exigida pela
nascente fé do Islã. Grandes progressbs em astronomia, arquitetura e alquimia
foram conseguidos pelos árabes, que antes estavam muitos séculos atrás de suas
contrapartes européias.
Por volta do século
XI, todavia, com a emergência de estados nacionais relativamente estáveis, as
técnicas de construção na Europa chegaram a um alto ponto de perfeição no
estilo românico. sobrepujando até mesmo as melhores obras apresentadas pelo
velho Império Romano. A construção com largos arcos fora dominada e os
construtores haviam aperfeiçoado tanto as junções de argamassa, que um cronista
do século XII comentou que as pedras da catedral de Old Sarum. iniciada em 1.102,
estavam tão bem colocadas, que se poderia pensar que toda a obra fora feita com
uma única rocha.
A esse elevado nível
de perfeição somou-se um novo elemento - o arco pontiagudo, uma revolução
geométrica originária da arquitetura sagrada islâmica. Afirma-se que o arco
pontiagudo teve origem, na Europa, no mosteiro beneditino italiano de Monte
Cassino, construído entre 1066 e 1071. Alguns, se não todos eles, dentre os maçons
que trabalharam nesse projeto eram cidadãos de Amalfi, uma república comercial
italiana que possuía postos comerciais em lugares tão distantes quanto Bagdá.
Com esse intercâmbio, foi só uma questão de tempo até que os segredos da
geometria dos maçons árabes fossem incorporados à arquite'ura sagrada
ocidental para formarem um novo estilo transcendente - agora conhecido
universalmente por gótico, nome pejorativo que lhe foi dado no século XVIII.
O arco pontiagudo que
introduziu essa revolução é produzido pela intersecção de dois arcos. Em sua
forma perfeita, esse arco é a metade posterior do vesica piscis. É estranha a
coincidência de que o patrono de Amalfi seja Santo André. Aquilo que é tido
como suas relíquias ainda repousa lá e sua efígie dourada segura um peixe - o
emblema do vesica.
Embora os pacíficos
comerciantes de Amalfi importassem o arco pontiagudo, os ou'ros segredos maçônicos
do Islã não foram conseguidos sob a égide do comércio. A 27 de novembro de
1095, o Papa Urbano II conclamou a cristandade a liberar os lugares santos e devolvê-Ios
ao cristianismo. Milhares de homens piedosos, sacerdotes, monges, mercenários,
soldados regulares e oportunistas atenderam ao chamado do Pontífice. A Primeira
Cruzada foi surpreendentemente bem sucedida. Nicéia foi capturada em 1097; no
ano seguinte caiu Antióquia e a 15 de julho de 1099 a cidade santa de Jerusalém
rendeu-se aos exércitos do Cristianismo após um cerco de apenas seis semanas.
Com esse sucesso sem
precedentes, os "francos", como eram conhecidos os cristãos
ocidentais, prosseguiram na obra de consolidação de suas conquistas. Como na
Inglaterra, trinta anos antes, o país conquistado foi tornado seguro para os
novos senhores por meio do reforço de velhos castelos e com a construção de
novos em pontos estratégicos por todo o país. Os maçons empregados para a construção
desses castelos utilizaram o trabalho escravo, que sem dúvida incluiu uma
proporção de maçons árabes, pois seus desenhos incorporam muitas características
desconhecidas dos artífices europeus.
A elasticidade e o
entusiasmo dos maçons daquele período são mostrados pela rapidez espantosa com
que as novas idéias conquistaram a Europa. A estrutura complexa da abóbada de
pedra reforçada com traves, conhecida apenas na Pérsia e na Armênia antes do ano
1100, foi utilizada na distante Catedral de Durham já em 1104. Fm Gales, a
Abadia de Neath foi construída por um dos maçons do rei Henrique I, Lalys,
um prisioneiro de guerra sarraceno. Suas téc nicas, aprendidas no Oriente
Médio' de uma tradição isolada, foram sem dúvida transmitidas aos maçons
ingleses e galeses que trabalharam com ele nesse projeto.
Outro elemento
importante na nova síntese foi a redescoberta das obras de Euclides, o geômetra
grego antigo. Sua obra fora considerada perdida para a Europa com a queda do
Império Romano e sobrevivera apenas nas traduções árabes. Por volta de 1120, o
eru dito inglês Adelard of Bath fez uma tradução dos Elementos do árabe
para o latim, que os tornou acessíveis pela primeira vez aos geômetras e
maçons europeus. O modo de transmissão dessa obra seminal para a Inglaterra não
é conhecido, mas os Cavalheiros Templários, que eram o repositório de muito do
saber arcano tradicional, podem tê-Ia obtido de uma fonte conquistada.
Edward W. Cox, um geômetra de Liverpool, escreveu em 1890:
"Durante o período
das Cruzadas, muitas das regras e muitos dos mistérios conhecidos nos tempos
clássicos parecem ter sido reorganizados. A influência da ocupação da Síria
sobre a arquitetura européia é muito marcada e maravilhosa. Não só incontáveis
igrejas, castelos e outros edifícios foram erigidos na Palestina pelos
invasores com a ajuda dos habilidosos operários sírios, mas também os
Templários e outras ordens militares e religiosas, que constituíram
estabelecimentos na Europa. trouxeram esse conhecimento oriental.”
Ao longo dos séculos
XII e XIII, foram desenvolvidas e refinadas as primeiras formas góticas. Os
métodos islâmicos foram estudados e incorporados numa nova linguagem formal
que passou de mão em mão com uma explosão de simbolismo místico. As grandes
catedrais dessa época, como as de Chartres e de Paris, apareceram numa forma
completamente nova num tempo consideravelmente curto. Sua construção,
executada com um fervor literalmente religioso, continua sendo uma proeza
espantosa de organização.
Uma tradição isolada,
mas paralela, da arquitetura de igrejas estava seguindo seu curso.
Conquanto as igrejas redondas configurem um tema contínuo, embora fragmentado,
ao longo de toda a arquitetura sagrada do mundo cristão, elas ocupam um lugar
especial e um pouco herético no esquema da geometria sagrada. O edifício redondo
ocupou um lugar especial na iconografia cristã pois fora a forma escolhida para
o Santo Sepulcro que uma vez marcara o sítio do túmulo de Cristo e o centro do
mundo. Com a forma circular desses edifícios representasse a reprodução
microcósmica do mundo, as igrejas redondas representavam em toda parte os microcosmos
locais que ocupavam o omphalos geomântico local.
As igrejas redondas
derivaram originalmente dos templos pagãos primitivos da mesma forma. Os templos
romanos redondos de Tivoli e Spalato, que sobreviveram até os tempos modernos,
são típicos dos santuários que inspiraram os geômetras sagrados cristãos. O
templo de Tivoli foi baseado no modelo grego, com colunação externa, mas o de
Spalato, que fazia parte do complexo do palácio do poderoso imperador pagão
Diocleciano, possuía colunas internas. Esse templo, planejado segundo o
octógono, como muitas igrejas templárias posteriores, formou o protótipo
desses santuários cristãos primitivos tais como o de San Vitale em Ravena, que
por sua vez jnfluiu sobre o Santo Sepulcro em Jerusalém e a capela de Carlos
Magno.
Como os templos
pagãos, as igrejas redondas eram microcosmos do mundo. Na Idade Média tardia,
elas tornaram-se a prerrogativa de uma seita enigmática e herética, os
Cavalheiros Templários. Esse corpo foi constituído em 1118 em Jerusalém com a
função aparente de prover proteção aos peregrinos que visitavam os santuários
da Cristandade na Terra Santa recém-conquistada. Seu poder cresceu rapidamente
e logo a ordem tornou-se fabulosamente rica e capaz de erigir capelas e igrejas
por toda a Cristandade. A forma redonda da igreja tornou-se especialmente
relacionada à ordem e no centro das rotundas de suas igrejas não havia um altar
sequer, mas um cubo perfeito de pedra talhada que era um dos mistérios do
Templarismo.
A ordem foi extinta
em 1314 e muitos dos seus oficiais mais graduados foram sentenciados à pena de
morte pelas autoridades da igreja. Sua vasta riqueza foi remetida aos cofres
dos monarcas do país em que a ordem funcionava. Mas, antes da extinção, a
fortuna dos Templários possibilitara a ereção de inúmeras igrejas redondas.
John Stow, em The Survey of London, 1598, escreveu: "Muitos homens nobres
em todas as partes do mundo tornaram-se irmãos dessa ordem e construíram
templos em toda cidade ou município da Inglaterra, mas o de Londres era sua
casa principal e fora construído segundo a forma do templo que está próxima do
sepulcro de Nosso Senhor em Jerusalém; eles possuíam outros templos em Cambridge,
Bristow, Canterbury, Dover, Warwick".
Apenas seis igrejas
redondas sobrevivem nas Ilhas Britânicas, duas das quais em ruínas. As outras
quatro foram reconstruídas em grande medida no último século. As igrejas de
Londres, Northampton e Cambridge foram construídas segundo o princípio
octogonal. A de Little Maplestead, em Essex (que pertenceu aos Cavalheiros
Hospitaleiros, organização-irmã dos Templários), foi construída segundo o
princípio hexagonal. No continente, a famosa capela de Drüggelte, na
Vestfália, foi feita de acordo com um plano de doze lados, e a igreja redonda
de Nijmegen, nos Países Baixos, incorporou uma estrutura de 8 e de 16 lados.
Essa igreja possuía um octógono central a partir do qual se construiu uma nave
lateral em dezesseis lados por meio de uma geometria simples.
Em Altenfurt, perto
de Nuremberg, na Alemanha, havia uma igreja que representava a forma mais
simples da arquitetura eclesiástica redonda. Consistia de uma nave redonda com
uma abside simpIes oposta à entrada. Nas Ilhas Órcades, também, em Orphir, existia
uma igreja redonda quase idêntica conhecida como Casa Girth. Foi quase
totalmente demolida no século XVII para fornecer material para uma nova capela
presbiteriana a ser construída perto dali. Ela existe apenas como um fragmento,
apresentando intacta apenas a abside. Todavia, seu nome dá-nos uma chave para a
sua função microcósmica. No antigo escocês, a palavra Girth ou Gyrth tinha o
significado de "santuário" ou "asilo". Girth também era
usada para designar um círculo de pedras que cercava um antigo local de julgamento.
Isso indicava que a igreja redonda de Orphir pode ter substituído um círculo de
pedras que ocupava anteriormente o seu sítio. A palavra Girth também é cognato
de garth e yarth, que significam terra, uma designação pública do microcosmo.
As igrejas redondas
pertencem a uma tradição separada da corrente principal da geometria sagrada
eclesiástica, tendo precedentes mais -nos esquemas romanos do que nos
românticos. Elas eram de alguma maneira especiais, reservadas para
sítios-omphalos importantes e não eram localizadas a esmo por todo o
território. Com a extinção dos Templários, a forma redonda da igreja foi
efetivamente eliminada até que a Renascença a redescobrisse diretamente nas
fontes pagãs antigas. Mas foi novamente suprimida quando as autoridades da
Igreja reconheceram suas origens pagãs.
Em 1861, a forma
redonda ainda era considerada pagã. O Reverendo J. L. Petit escreveu nesse ano:
"Quase todos os
espécimes continentais [de igreja redonda] são considerados pelos habitantes do
lugar como um templo gentio; e, embora em cada caso particular não seja
necessário refutar a suposição, a universalidade da tradição pode torná-Ia
digna de nota do antiquário. E, se for necessário procurar a derivação de uma
forma tão simples, não há dúvida de que, como a forma retangular, ela pode ser
remontada à época do paganismo.”
Mas por que a forma
redonda da igreja foi considerada não-cristã pela hierarquia da Igreja? A
forma redonda, ao contrário de outros padrões tais como a Cruz Latina, não
representava o corpo de um homem ou o corpo de Deus. Ao contrário, representava
o mundo, o domínio do terreno, e, em termos cristãos, as forças satânicas, pois
que o Diabo na época medieval era personificado como Rex Mundi, rei do mundo.
No costume Templário, essa terrenidade era enfatizada pelo cubo que se situava
no centro mesmo da rotunda. O cubo no interior do círculo representava a
terra nos céus, a fusão dos poderes considerados heréticos pelos cristãos medievais,
donde a perseguição aos alquimistas, magos e heréticos que se empenhavam nessa
fusão. Com esse simbolismo exposto, não foi difícil provar a acusação de
heresia com que os infelizes Templários foram incriminados. Princípios
jslâmicos públicos, derivados da ala mística do maometanismo, os Sufis, só serviram
para amaldiçoar ainda mais a seita.
Todavia, o
conhecimento técnico islâmico era de outra natureza. Sobreveio, por meio de um
estranho conjunto de circunstâncias, um segundo período de influência islâmica
que deveria varrer o gótico "puro" de Chartres. Durante o século
XIII, as hordas mongóis saíram de sua base na Ásia Central e se converteram
numa séria ameaça ao Oriente Médio e à Europa. Após a primeira fase da
expansão, o Império Mongol estava consoljdado com seu posto avançado na Pérsia
sob o governo de um vice-rei que atendia pelo título de IIkhan. Tendo deixado
de representar uma ameaça à Cristandade, os mongóis logo foram vistos como
aliados contra os turcos. Vários reis cristãos enviaram emissários a sucessivos
IIkhans a fim de cultivar essa aliança. Digno de nota foi o Olkhan Arghun (1284-1291),
que manteve relações com muitos estados cristãos. Ele chegou até mesmo a enviar
uma embaixada a Londres em 1289. Em troca, o rei Eduardo I da Inglaterra enviou
uma missão comandada por Sir Geoffrey Langley à Pérsia. Langley participara de
uma cruzada com o rei no começo dos anos 70 e viajara à Pérsia via
Constantinopla e Trebizonda em 1292. Tajs embaixadas eram um canal para a
transmissão do novo conhecimento. Os arquitetos asiáticos misturaram as suas
técnicas com a tradição islâmica persa e aos poucos seu estilo foi transformado
pelos maçons geômetras europeus.
Um edifício do
período IIkhan que exerceu um efeito notável sobre a Europa foj o famoso
mausoléu do IIkhan Uljaitu, em Sultaneih. No início deste século, o erudito
alemão Ernst Diez fez um estudo exaustivo desse memorial. Toda a sua estrutura
é determinada por dois quadrados interpenetrados que formam um octógono. A
partir dessa base octogonal, derivou-se a elevação, que contém triângulos e
quadrados. A altura do edifício, medida por M. Dieulafoy rios anos 80 do
século passado, é de 51 metros e o diâmetro interno tem exatamente a metade. Um
sistema de razões, derivadas geometricamente, foi a origem básica dessas
harmonias. Ao passo que o diâmetro principal dos pilares servira aos gregos antigos
como módulos, os arquitetos persas levaram as dimensões dos arcos ou domos a
relações determinadas com as outras partes do edifício. No mausoléu de Uljaitu,
o ponto básico de partida foi a dimensão do diâmetro interno da câmara
mortuária.
A partir dessa
dimensão, o arquiteto construiu um octógono para a planta baixa. Para a
elevação, um quadrado duplo foi erguido. No quadrado superior, um triângulo eqüilátero
definiu. o domo e o tímpano sobre o qual ele foi erguido acima da porção basal
cúbica. As câmaras laterais e as galerias foram determinadas geometricamente
por triângulos eqüiláteros cujas posições foram fixadas por quadrados oblíquos
e diagonais. A arquitetura do mausoléu representava um ponto de partida
construçional que influenciou o octógono da Catedral de Ely nas terras
pantanosas longínquas do East Anglia. Mausoléus com o teto como espigões do
domo não haviam aparecido antes na Pérsia, embora tivessem sido construídos na
velha Delhi. Os mesmos sistemas de geometria que os maçons europeus utilizaram
em seus grandes edifícios foram utilizados para glorificar um sistema religioso
bastante diferente. A origem oriental dessa geometria, todavia, não deteve
os arquitetos cristãos em sua tarefa. Como tecnólogos progressistas, eles
acolheram com prazer as novas idéias dos infiéis e as incorporaram às últimas
obras. Os princípios transcendentes foram adotados com alacridade pelos homens
pragmáticos, cuja compreensão do simbolismo os capacitara a trabalhar com o
inexperimentado e o insuspeitado.
O conhecimento
acumulado da Pérsia e de outros países do Oriente Médio foi logo aumentado com
informações provenientes de outros lugares. Em 1293, missionários cristãos
foram da Itália à China e em 1295 Marco Polo retomou a Veneza, vindo de Pequim.
Com esse intercâmbio sem precedentes, eram inevitáveis novas geometrias
sagradas. Um exemplo bastante bem documentado da influência oriental está no
Grande Salão da Piazza della Ragione, em Pádua. Foi desenhado por um frade
agostiniano chamado Frate Giovanni por volta de 1306. Giovanni trabalhara em
muitos lugares da Europa e da Ásia e trouxera planos e desenhos dos edifícios
que vira. Em Pádua, reproduziu um vasto teto de vigas que vira na Índia e que
media 240 pés por 84.
Outras influências
orientais podem ser demonstradas pelo aparecimento simultâneo de temas exóticos
em lugares bastante distantes entre si. O arco de gola, em que os arcos que
formam o arco são voltados para fora e continuam como uma característica arquitetônica
sobre a porta ou janela, apareceu simultaneamente sem antecedentes tanto em
Veneza quanto na Inglaterra. Detalhes da porta de St. Mary Redcliffe, em
Bristol, e também na catedral dessa cidade e no castelo de Berkeley, também
apresentam uma influência oriental inconfundível que pode ser comparada com a
obra de Lalys em Neath.
As visitas de
registradores desses detalhes arquitetônicos locais, tais como as de Simon
Simeon e Hugh, o Iluminador, na Terra Santa em 1323, serviram para reforçar o
interesse nos círculos monásticos pelo desenho oriental. O estilo
"perpendicular" na Inglaterra, que surgiu por volta do final do
século XIV, foi prenunciado pelos hexágonos alongados nos edifícios muçulmanos
egípcios do século XIII. Os elementos verticais que cruzam a curva de um arco,
uma característica importante do desenho da Capela do King's College em
Cambridge (iniciada em 1446), já existiam no Mausoléu de Mustapha Pasha no
Cairo, construído entre 1269 e 1273. Os maçons da Europa, embebidos em
conhecimentos geométricos, assimilaram prontamente as técnicas da arquitetura
simbólica do Islã, realçando-a e trazendo-a a uma nova era.
9.
Simbolismo Maçônico e Prova Documental
"As
linhas geométricas falam a linguagem da crença - da crença forte, apaixonada,
duradoura. Nelas as leis eternas da proporção e da simetria reinam supremas. O
ciclo daquilo que é gerado divinamente está reproduzido na linguagem numérica
do coro, do transepto, da nave, do corredor, do portal, da janela, da coluna,
da arcada, do frontão e da torre. Toda característica tem sua unidade de medida,
seu simbolismo místico.”
Hermon
Gaylord Wood - Ideal Metrology.
As catedrais
medievais são a mais fina flor da arte da geometria sagrada que se desenvolveu
na Europa. As manifestações físicas da summa theologiae, a incorporação
microcósmica do universo criado, as catedrais em sua forma completa perfeita,
unidas em suas posições, orientações, geometria, proporção e simbolismo, tentam
criar a Grande Obra - a unificação do homem com Deus. Tem-se observado que
muitas catedrais, como as de Canterbury, Gloucester e Chartres, foram
construídas no sítio de antigos círculos megalíticos, incorporando em seus
desenhos o posicionamento e a geometria dos círculos. Geomanticamente situados
de maneira a poderem empregar ao máximo as energias telúricas da terra e as
influências astrofísicas dos céus, os círculos de pedra derrubados pelos
zelosos santos cristãos foram amalgamados na estrutura mesma das igrejas que
os sucederam.
Louis Charpentier
sugeriu que as pedras antigas de estruturas megalíticas, além de absorverem
influências cósmicas e telúricas, também agiam como instrumentos de vibração.
Esses instrumentos de pedra, afirmou ele, podiam acumular e ampliar as
vibrações das ondas telúricas, agindo antes como uma caixa de ressonâncja.
Essas energias, assumidas pelos cristãos, ainda exigiam um ressonador, que foi
providenciado com a construção das paredes de pedra e da abóbada da catedral.
Se a geometria dos
círculos e dolmens de pedra dependia do comprimento da onda das energias
telúricas, então a geometria, reproduzida num vasto edifício de pedra, agiria
como um canal para as energias ressoantes ali capturadas. As lendas que cercam
a fixação das energias da terra no omphalos e que estão incorporadas aos contos
universais de matadores de dragão reforçam este ponto de vista. Nos mitos de
morte do dragão, o herói solar transpassa o dragão com sua espada ou lança.
Fazendo-o, ancora as energias telúricas vagueantes da Terra em um sítio, de
maneira que elas possam ser contidas e canalizadas para uso do sacerdócio. Nos
últimos tempos, o herói solar identificou-se com os santos cristãos Jorge e
Miguel.
Outra indicação desse
fenômeno é a aceitação universal da medida canônica. Em muitas culturas, não se
acreditava que as unidades fundamentais de medida possuíssem origens divinas,
mas tinham sido transmitidas pelos Deuses. O receptáculo dessas medidas
sagradas era um homem ou um semideus, freqüentemente o fundador legendário da
nação. Essas medidas eram então cuidadosamente guardadas contra a profanação e
a alteração e largamente empregadas na construção da arquitetura sagrada.
Assim, vemos as proporções serem engendradas naturalmente pela geometria a
partir da medida inicial. Se a catedral era destinada a agir como um canal e um
ressoador, não se poder,ia escolher nenhuma dimensão melhor do que aquelas
baseadas num sistema harmônico natural elaborado com medidas diretamente
relacionadas ao comprimento telúrico das ondas. O comprimento da onda das
energias telúricas locais, uma vez determinado por métodos ocultos, podia ser
venerado em medidas sagradas imutáveis e formar uma base natural para a
construção dos instrumentos que deveriam manipular essas energias.
Charpentier
acreditava que os beneditinos intensificavam as forças terrestres por meio do
som físico - o canto gregoriano -, cuja ação aumentava a harmonia
geométrica do edifício para a produção de estados mais elevados de consciência.
Os beneditinos eram, na verdade, uma ordem que utilizava o conhecimento antigo.
O pesquisador alemão Kurt Gerlach descobriu que os mosteiros beneditinos da
Boêmia (Tchecoslováquia) foram arranjados uns com os outros segundo relações
geométricas precisas. Esses mosteiros estavam localizados em linhas segundo
múltiplos e submúltiplos específicos da medida antiga conhecida como Raste,
correspondente a 44 quilômetros.
Assim, as várias
características da catedral gótica eram harmonizadas para criarem um todo que
ligava completamente o homem, o microcosmo, com o universo. As funções
múltiplas que se esperavam as catedrais góticas cumprissem significavam que
elas não seriam apenas expressões de harmonia geométrica simples como a Saint
Chapelle em Paris ou a Capela do King's College em Cambridge. Elas
necessitavam várias divisões e subdivisões que cumprissem as funções de local
de encontro, igreja da paróquia, capela para ofícios menores, confessionário e
sede do Bispado local. Além desses usos exotéricos, a catedral tinha de incorporar
as doutrinas da fé e expressar as energias e geometrias inerentes ao sítio.
Assim, as geometrias das catedrais góticas incorporam muitas estruturas
complexas que podem ser interpretadas em vários níveis. A geometria
fundamental da planta baixa é sempre gerada diretamente da linha axial
orientada. A data da fundação e a sua orientação são "trancadas" na
geometria à aparente posição solar no dia do padroeiro. Assim, em cada dia
patronal sucessivo, o sol brilharia diretamente ao longo do eixo da catedral. O
Professor Lyle Borst descobriu que muitas catedrais possuem uma geometria do
lado leste derivada dos círculos de pedra. As orientações desses sítios megalíticos
segundo vários fenômenos solares e lunares são bastante conhecidas,
pesquisadas que foram por estudiosos como Sir Norman Lockyer e o Professor Alex
Thom. A geometria das catedrais, que recobre a das orientações múltiplas dos
círculos de pedras, também devia preservar orientações outras que não a simples
orientação axial do dia do p'adroeiro. Isto também quer dizer que o padroeiro
pode ter sido determinado a partir da orientação principal do círculo de pedra
preexistente.
Descobriu-se
recentemente que o esboço do vasto complexo de templos de Angkor Wat, no
Camboja, foi desenhado de tal maneira que fossem incorporados 22 alinhamentos
separados de posições solares e lunares. Observando os fenômenos de alguns
pontos bem determinados, o astrônomo-sacerdote era capaz de checar o calendário
por meio da observação direta. A construção das catedrais britânicas no topo de
observatórios megalíticos pode ter reproduzido de maneira similar a informação
astronômica em sua geometria. Rose Heaword demonstrou que a Capela de St. Cross
em Winchester possuía um alinhamento nascer-do-sol que era visível em determinado
ponto por uma janela. Esse nascer-do-sol ocorre no dia da Santa Cruz, a 14 de
setembro, e não corresponde à orientação axial da capela. Estudos que estão
sendo efetuados podem demonstrar muito mais a respeito desses alinhamentos
múltiplos e de sua relação com a geometria sagrada.
No período em que as
catedrais góticas foram erigidas, havia dois sistemas maçônicos de geometria
que eram comumente usados. O mais antigo era conhecido como ad quadratum e
baseava-se no quadrado e nos seus derivados geométricos. O mais novo, e em
alguns aspectos o sistema mais dinâmico, baseava-se no triângulo eqüilátero e
era conhecido como ad triangulum.
O ad quadratum era
formado diretamente do quadrado e da sua figura derivada, o octograma.
Colocava-se por cima do quadrado inicial - que era orientado segundo a maneira
aprovada pelos geomantes e maçons encarregados da orientação - um segundo
quadrado do mesmo tamanho. Este, a um ângulo de 450 do primeiro quadrado,
formava o octograma, um poligrama de oito pontas. Na tradição maçônica,
essa figura foi inventada por um mestre de Estrasburgo, Albertus
Argentinus. Nos escritos maçônicos alemães posteriores, essa figura é chamada
acht-uhr ou acht-ort, oito horas ou oito lugares. Esses nomes aludem a uma
divisão óctupla pagã antiga do compasso, o dia e o ano que eram imitados no
edifício como um microcosmo do mundo. A partir desse octograma inicial, toda a
geometria da igreja podia ser desenvolvida de duas maneiras.
A primeira maneira, o
acht-ort verdadeiro, desenvolvia uma série de octogramas internos e externos,
traçados diretamente a partir da primeira figura. Esse sistema. pode ser visto
nas catedrais de Ely (ver Figura 26), Verdun, Bamberg e em outras catedrais
basicamente românicas. Todavia, à época das últimas igrejas góticas, o sistema
ad quadratum refinou-se para uma forma mais complexa baseada mais no quadrado
duplo do que no simples. Essa forma, deve-se lembrar, era favorecida desde a
antigüidade egípcia como uma forma adequada a um lugar santo.
A segunda e última
derivação do ad quadratum produziu o complexo geométrico elegantemente
proporcionado conhecido como "dodecaid", um poligrama irregular de
doze pontas que se prestou admiravelmente ao planejamento de igrejas. Como o
acht-ort simples do ad quadratum primitivo, a figura básica era um octograma.
Todavia, o primeiro quadrado, do qual se derivava o octograma, era ampliado até
formar um quadrado duplo e, desse segundo quadrado, construía-se outro
octograma. Isto fazia uma figura de dois quadrados contíguos com quadrados
coincidentes a 450 do quadrado duplo. Sobre esse octograma interlaçado
sobrepunha-se um quadrado maior que cortava as intersecções internas dos dois
octogramas. Isso produzia uma figura que possuía razões geométricas que se
interseccionavam na construção.
O dodecaid é rico em
simbolismo cristão. Os três quadrados coincidentes possuem em seu centro um
pequeno quadrado comum a todos eles. O quadrado central é maior do que os
outros, simbolizando o Pai da Trindade Cristã, com o quadrado pequeno no meio
simbolizando a unidade essencial da divindade trina. A estrutura do quadrado
duplo que penetra a trindade incorpora os quatro elementos e as quatro direções.
simbolizando o mundo material interpenetrado e sustentado pela divindade. O
todo é uma sinopse dos números três e quatro, o sete místico.
Na construção atual
da igreja, os quatro cantos do quadrado duplo marcam as quatro fundações da
igreja, as pedras angulares sobre as quais se funda a construção material. O
mais oriental dos três 45° representa Cristo. Seu centro é o foco onde o altar
é fundado e onde, a cada dia, por meio da celebração da Missa, acreditam os
cristãos, Cristo está presente na forma de hóstia e de vinho. O quadrado maior
e central, no oeste, representa o pai. Baseia-se no omphalos central, o ponto
do cruzamento sobre o qual a torre principal e a agulha deverão ser erguidas.
Esse centro, o ponto coincidente dos três quadrados que representam a fusão da
trindade, indicava freqüentem ente um poderoso centro geomântico. Esse centro
pode ser percebido pelos hidróscopos sob a forma de uma poderosa fonte
cega com suas espirais associadas. Esse omphalos geomântico existe na Catedral
de Salisbury, que possui a agulha mais alta da Inglaterra e marca um lugar
situado numa linha ley que vai de Stonehenge a Frankenbury. Mais a oeste da
cruz da catedral está o quadrado que representa o Espírito Santo. Aqui, -
tradicionalmente, ficava a pia batismal, o lugar em que o Espírito Santo
penetrava no neófito por ocasião do seu batismo.
A essência da
geometria sagrada é simples. Todas as partes 90 conjunto sagrado, desde o
aparato e as vestimentas do clero até a forma de todo o edifício sagrado, são
determinadas diretamente por uma figura geométrica fundamental. Todas as dimensões
e todas as posições estão idealmente relacionadas diretamente a esse sistema
e, assim sendo, estão integradas com o todo da criação. As elevações das
igrejas medievais eram determinadas diretamente pela geometria das plantas
baixas. A Saint Chapelle, a capela dos reis franceses, demonstra admiravelmente
essa necessidade geométrica. Sua planta baixa é produzida pelo dodecaid, com
uma pequena capela lateral feita a partir de uma versão menor do ad quadratum
e a sua geometria elevacional interna feita diretamente a partir deste último.
Edifícios posteriores, como a capela do King's College, foram planejados pelos
mesmos métodos, mas as dimensões, em vez da geometria direta, foram dadas pelas
autorizações dos seus planos. Assim, a altura da abóbada de King's College foi
mantida na capela terminada, embora tivesse sido seguido um método de
construção da abóbada diferente do que fora pensado anteriormente.
As igrejas medievais
não foram desenhadas apenas como galpões que acomodassem um determinado número
de fiéis; nem, como se deduz freqüentemente, foram construídas "à medida
que eram erigidas". Exatamente como na prática arquitetônica moderna, tudo
era calculado para fazer avançar cada detalhe, toda e qualquer característica
do edifício era determinada exatamente de acordo com a geometria sagrada. As
peças sobreviventes apresentam uma preocupação, por parte dos desenhistas, com
dimensões e proporções precisas.
A planta baixa da
Catedral de Ely, em Cambridgeshire, servirá para ilustrar os trabalhos práticos
da geometria sagrada medieval. Como muitos outros edifícios, a catedral atual é
o resultado de muitos séculos de acréscimos. A catedral normanda original
foi esboçada em 1082 e completada cerca de um século mais tarde. No século
XIII, foi acrescentado um pórtico na extremidade oeste, na mesma posição do das
catedrais de Glastonbury e Durham. Na mesma época, foi feita uma extensão para
o leste do coro com dimensões definidas de acordo com os princípios do ad
quadratum. A extensão foi definida por um quadrado oblíquo da largura da nave
mais um triângulo de 45° da largura da abóbada. Esse quadrado oblíquo foi
utilizado mais tarde para determinar a largura da nova Lady Chapel, que foi
iniciada em 1321.
As dimensões da Lady
Chapel não foram definidas pelo ad quadratum, mas pelo mais recente ad
triangulum maçônico. Suas dimensões foram produzidas pela geometria de um
círculo cujo raio é um pouco menor de 105 pés ingleses (96 pés saxônicos). Este
é o raio que def.iniu o octograma básico com que se esboçou a planta baixa da
catedral. O canto interno do nordeste de Lady Chapel foi produzido por raios
interseccionantes da mesma extensão, como também o canto noroeste, que também
foi marcado pelo quadrado oblíquo. A linha diagonal que define o espaço
oriental da catedral chega ao canto noroeste de Lady Chapel depois de passar
pela porta da capela. Um raio do centro do cruzamento que toca os arcobotantes
da extremidade leste do coro também toca os arcobotantes de Lady Chapel. Seu
raio tem 192 pés saxônicos - o dobro do raio da base do octograma, gerado pela
geometria ad quadratum.
No ano seguinte ao
início de Lady Chapel ocorreu um desastre. A torre central, situada sobre o
cruzamento, ruiu para o leste, talvez enfraquecida pelas operações da
construção. A reconstrução foi iniciada e seguiu-se a geometria sagrada
original do ad quadratum. A velha - torre não foi copiada, mas um novo domo
gótico octogonal, sem precedentes na arquitetura ocidental, foi erigido em seu
lugar. O método técnico de construção foi uma cópia quase exata daquele que fora
utilizado no mausoléu persa de Uljaitu Chodabendeh em Sultaneih. Sobre esse
octógono de pedra sem precedentes foi construído um incomparável
"farol" de madeira, desenhado e executado pelo Carpinteiro Real,
William Hurley. No seu centro está uma magnífica obra de talha, representando
Cristo em Majestade, executada por John Burwell. Exatamente acima do
cruzamento, ela representa a contraparte celestial do omphalos terreno.
Embora tenha
sobrevivido muito pouca documentação sobre as construções românicas tardias ou
góticas primitivas, os detalhes documentais de duas tardias e notáveis igrejas
colegiadas medievais ainda podem ser examinados. A ,igreja de Fotheringhay, em
Northamptonshire, e a Capela do King's College, em Cambridge, foram construídas
segundo instruções precisas que ainda sobrevivem.
Ambos os edifícios
foram desenhados no século XV. Fotheringhay é o mais antigo dos dois. A aldeia
de Fotheringhay é hoje notável apenas por seu cenário pitoresco entre as
campinas banhadas pelo rio Nene e pela espantosa torre octogonal de uma igreja cujo
desenho memorável mostra sua eminência anterior. A forma isolada da igreja
lembra-nos tristemente que ela é agora apenas um fragmemo de um colégio reai,
reduzido hoje à condição de paróquia. O colégio foi fundado por Edward
Plantagenet, apelidado Langley, o quinto filho do rei Eduardo III. Edmundo,
Duque de York, seria o fundador da Casa de York. Ele iniciou a construção do
colégio e reconstruiu a igreja paroquial, que estava ligada a ele por um
claustro de 88 janelas de vidro colorido. O filho de Edmundo, Eduardo, Duque de
York, pretendia levar à frente o projeto após a morte do seu pai com a
reconstrução da nave da velha igreja no mesmo estilo do novo coro, mas foi
morto na batalha de Agincourt antes que a construção fosse iniciada. Todavia,
o projeto não foi abandonado e é o exame de um acordo assinado a 24 de setembro
de 1434 que nos informa sobre as práticas maçônicas de desenho dos franco-maçons
ingleses daquela época.
O contrato foi feito
entre William Wolston, Squire, e Thomas Pecham, amanuense, comissários do
"Supremo e poderoso príncipe, meu Senhor respeitável, o Duque de
York", e WiIliam Horwood, franco-maçom de Fotheringhay. O contrato
detalhava com medidas precisas a especificação de uma igreja cujas proporções
requintadas ainda hoje deliciam os olhos. O contrato estipulava a construção de
"uma nova nave de uma igreja, que chegue até o coro, no Colégio de
Fotheringhay, da mesma altura e da mesma largura do dito coro; e que tenha um
comprimento de oitenta pés a partir do dito coro, com paredes de um
metro-jarda (de espessura), um metrojarda da Inglaterra, contado sempre como
três pés. (...) E no lado norte da igreja o dito William Horwood fará um
pórtico; o lado externo de pedra de cantaria lisa, o lado interno de pedra
áspera, contendo em comprimento doze pés e em largural o que o arcobotante da
nave permitir (...) e na extremidade oeste da dita nave haverá um campanário
construído sobre a igreja sobre os três arcos fortes e poderosos abobadados em
pedra. Dito campanário terá de comprimento oitenta pés segundo o metro-jarda de
três pés para uma jarda, sobre o chão a partir das pedras da cornija e vinte
pés quadrados entre as paredes (...)".
Cada detalhe do
edifício proposto foi especificado no contrato, e também as dimensões quando
elas foram julgadas relevantes. Não se- sabe se o próprio Horwood projetou as
dimensões e esboçou um diagrama que serviu de base para as dimensões contratuais.
Só doze anos depois é que uma outra fundação colegiada real apontaria para a
possibilidade de o fundador ou seus auxiliares diretos no campo geomântico
terem executado o desenho. Seja qual for a verdade, o tom de todo o contrato
está vazado como instruções a Horwood, o franco-maçom funcionário que está apenas
recebendo ordens de uma autoridade superior, e não detalhes elaborados
arbitrariamente por ele.
Embora a igreja de
Fotheringhay tivesse sido completada por volta de 1460, data da morte de
Ricardo, o Duque de York, a construção da abóbada abaixo da torre traz a marca
do grande mestre lohn WastelI, de quem uma obra idêntica sobrevive hoje na
Catedral de Peterborough, na porta de entrada de St. John's ColIege em
Cambridge e, sobretudo, no teto magistral da Capela do King's College, na mesma
cidade.
Essa capela foi
desenhada pelo rei Henrique VI, o fundador. Na sua declaração de intenções,
datada de 1498, ele forneceu todas as dimensões necessárias a que seu mestre
maçom, Reginald Ely, preparasse os planos completos para a capela e, por
conseguinte, todo o colégio. Uma análise dos seus planos mostra que eles foram
baseados no ad triangulum. Todas as partes da capela estão relacionadas com a
geometria global, até mesmo as pequenas capelas anexas laterais. Embora 69
anos se tenham passado antes que a capela fosse completada, o mestre maçom John
Wastell, que não havia nascido quando a capela foi iniciada, aderiu à letra da
declaração de Henrique terminando-a exatamente nas dimensões estipuladas. O
sistema geométrico, a despeito das alterações de características dinásticas e
estilísticas, foi mantido como dever sagrado.
10.
Problemas, Conflitos e Divulgação dos Mistérios
"A
história antiga é como uma paisagem noturna, na qual andamos às apalpadelas,
discernindo vagamente alguns contornos na escuridão geral, e ficamos felizes se
aqui ou ali a obra de um autor em particular ou uma ruína ou uma obra de arte
ilumina momentaneamente, como um raio nas trevas, o campo particular que
estamos explorando.”
Filo,
Sobre a vida contemplativa.
O caso da construção
da Catedral de Milão é de extrema importância no estudo da geometria sagrada.
Ele interessa em dois sentidos, o documental e o simbólico. A Catedral de Milão
foi fundada em 1386 e, por essa razão, estava no centro de uma encarniçada
controvérsia relativa a que forma de geometria sagrada deveria ser utilizada:
ad quadratum ou ad triangulum. Um grande número de peritos reuniu-se a fim de
determinar o que seria feito na construção dessa obra-prima potencial. Talvez
por causa dessa pletora de peritos, desenvolveu-se entre os adeptos de um e de
outro sistema uma encarniçada discussão.
Sabe-se que já em
1321, durante a ereção do domo da catedral de Siena, os cinco inspetores
escolhidos para examinar a construção objetaram contra a continuação da obra
"porque, se terminada como foi iniciada, ela não terá as medidas de
comprimento, largura e altura que as regras prevêem para uma igreja". Uma
disputa similar verificou-se a respeito da construção da Catedral de Milão.
Hoje, a Catedral de
Milão é considerada uma obra-prima da arquitetura gótica tardia. Recentemente,
sua estrutura foi algo sacudida pelas vibrações dos carros, dos ônibus e
do metrô que trafegam ao seu redor, mas a sua gestação foi tão cheia de recriminações
que parecia que ela nunca seria terminada. A catedral foi fundada em 1386 por
ordem de Gian Galeazzo Visconti, que conquistara influência sobre a cidade de
Milão graças ao expediente da morte do seu tio. Todavia, nenhum outro edifício tão
portentoso foi construído na Lombardia durante séculos e logo os maçons
inexperientes encarregados do projeto defrontaram se com sérios
problemas. O lado teórico da geometria sagrada segun do a qual o edifício
deveria ser construído atolou-se numa discussão aparentemente insolúvel.
Inicialmente, a
planta baixa da catedral fora desenhada de acordo com o ad quadratum, baseado
no quadrado e no quadrado duplo, com uma nave central pronunciada e naves
laterais de igual altura. Essa planta, todavia, foi logo abandonada e
substituída pelo ad triangulum para a elevação - e foi aí que os problemas
começaram. A altura de um triângulo eqüilátero, a base do ad triangulum, é incomensurável
com seu lado. Colocá-Io sobre uma planta baixa báseada no ad quadratum seria
transformar numa tolice a comensurabilidade da geometria sagrada e todas as
proporções da elevação estariam completamente erradas.
A fim de trazer
novamente um ar de lógica à geometria, foi chamado um matemático de Piacenza,
Gabriele Stornaloco. Ele recomendou um arredondamento da altura incomensurável
de 83,138 para 84 braccia, que poderia ser comodamente dividida em seis
unidades de 14 braccia. Embora fosse aceitável em princípio, o esquema de
Stornaloco foi posteriormente modificado, produzindo-se uma redução posterior
na altura e trazendo-se a catedral para mais perto dos princípios clássicos. O
mestre maçom alemão Heinrich Parler enfureceu-se com esse compromisso de
medida verdadeira. Seus protestos levaram-no a se demitir do posto de consultor
em 1392. Em 1394, Ulrich von Ensingen veio de UIm como consultor, mas ficou em
Milão apenas seis meses antes de fazer novamente as malas. Os maçons lombardos
lutaram desesperadamente até 1399, quando Jean Mignot foi chamado da França
para supervisionar as obras.
Mignot, todavia, não
ficaria aí por muito tempo. Suas críticas aos princípios maçônicos locais foram
tão causticantes, que um comitê foi chamado a discutir os pontos que ele
levantara. Uma tal ignorância dos princípios geométricos e mecânicos góticos
foi demonstrada pelos maçons lombardos, que eles tentaram argumentar que os
arcos pontiagudos não poderiam de maneira alguma justificar a geometria
aberrante pretendida para o edifício. Exasperado, Mignot bufou: "Ars sine
scientia nihil est" (A Arte não é nada sem a Ciência). Recebeu a seguinte
réplica lombarda: "Scientia sine arte nihil est" (A Ciência não é
nada sem a Arte).
Mignot voltou para
Paris em 1401, sem ter feito progresso algum com os intransigentes lombardos.
Por métodos pragmáticos, os italianos improvisaram e terminaram o coro e os
transeptos por volta de 1450. Nem toda a catedral foi terminada, todavia, até
que a fachada oeste foi finalmente completada sob as ordens do Imperador
Napoleão I em 1809.
A geometria de Milão
foi preservada numa edição de Vitrúvio publicada em 1521. Ela mostra o plano e a
elevação da catedral como uma ilustração dos princípios vitruvianos. Só esta
ilustração é uma prova da unidade essencial dos sistemas clássicos e maçônicos
da geometria sagrada. O esquema apresentado na gravura baseia-se no rhombus ou
vesica. A elevação triangular do corte transversal da catedral é mostrada em
superposição a círculos concêntricos em que o quadrado e o hexágono são
desenhados, demonstrando a relação da elevação com o ad quadratum do plano
básico.
Essa exposição da
geometria sagrada maçônica de uma catedral é indicativa da atitude modificada
diante dos mistérios antigos exibidos pelos escritores da Renascença. Ela se
encaixa perfeitamente na tradição de Matthäus Röriczer, um maçom que revelou
sua arte quebrando seu juramento de sigilo. Röriczer, que morreu em 1492,
pertencia à terceira geração de uma família que servia de mestres maçons na
Catedral de Regensburg. Matthäus era o chefe de uma loja onde fora desenhada e
executada toda a obra de construção e, como tal, era o responsável por todas as
molduras e todos os entalhes, por seu esboço e seu desenho. Embora, sendo um
franco-maçom, estivesse preso ao juramento horrendo de não divulgar os mistérios
maçônicos aos não-iniciados, ele deu um passo sem precedentes com a publicação
de detalhes que anteriormente haviam sido ocultados nos livros de
anotações das lojas maçônicas operativas.
Embora a única obra
publicada de Röriczer fosse um pequeno panfleto que deu solução a um problema
geométrico, ela tem uma importância fundamental porque é a única chave
sobrevivente da geometria sagrada maçônica. A obra, intitulada On the
Ordination of Pinnacles, forneceu a solução do problema de como erigir um
pináculo de proporções corretas a partir de uma planta baixa dada. Por volta do
final do período medieval, os maçons estavam produzindo as obras-primas do
gótico flamboyant e perpendicular pelos meios mais simples. As plantas de
execução (conhecidas na Inglaterra como "plats") eram preparadas
pelos maçons até os últimos detalhes. Ainda existem alguns desses
"plats", como os que foram desenhados para a fachada oeste da
Catedral de Estrasburgo, por Michael Parler em 1385, e o da agulha da Catedral
de Ulm, por Matthias Böblinger. Cada uma das partes do intrincado desenho
é relatada aos seus camaradas por meio da geometria. O maçom operativo,
equipado com esse diagrama, podia tomar uma dimensão como ponto de partida e
com ela, utilizando-se régua e compasso, a geometria chega ao plano do tamanho
natural das partes que ele deve executar. Com esse plano rdo tamanho natural,
desenhado sobre um "piso de decalque" de gesso, faziam-se gabaritos
de madeira segundo os quais as pedras finais eram cortadas e talhadas.
A exposição de Röriczer
do sistema demonstra admiravelmente a simplicidade elegante desse método
canônico. Em vez de uma referência constante a medidas num plano, como na
moderna prática da engenharia, o pináculo (ou o pinásio, a ombreira da porta, o
componente da abóbada, etc.) era "desenvolvido" organicamente, por
assim dizer, a partir de um quadrado. A geometria, diferentemente da medida, é
auto-reguladora e quaisquer erros podem ser vistos imediatamente. Seja qual
for o tamanho do quadrado inicial, todas as partes do pináculo estão
relacionadas a ele em proporção natural. Como as dimensões do quadrado original
poderiam ter sido derivadas como uma função da geometria global da igreja, o
tamanho do pináculo estava relacionado harmoniosamente ao todo.
O livreto de Röriczer
foi dedicado ao Príncipe Wilhelm, Bispo de Eichstadt (1464-1496), descrito
na dedicatória como "(...) um cultor e um patrono da arte livre da
geometria". Wilhelm era membro ativo do conselho de construções das
igrejas de Regensburg, UIm e Ingolstadt. Depois de termos lido a instrução de
Röriczer, não achamos que Wilhelm fosse apenas um administrador, mas uma pessoa
bastante interessada em conhecer a metodologia exata que estápor trás da
geometria sagrada. Esses homens foram os primeiros "maçons especulativos",
patronos ricos que desejavam sinceramente conhecer os segredos dos maçons operativos.
A fim de obter esses segredos, os patronos eram geralmente admitidos à irmandade
dos franco-maçons por meio dos ritos iniciatórios típicos. Como as atividades
dos maçons diminuísse com o surgimento de arquitetos treinados em academias, o
número de "maçons especulativos" aumentou.
Entrementes, as lojas
operativas de franco-maçons fecharam-se uma a uma. A última delas foi a
primeira loja da Europa - a de Estrasburgo, que fechou em 1777. A partir de
então, as artes e os mistérios da franco-maçonaria foram mantjdos apenas pelos
"maçons especulativos".
Os pináculos
descritos por Röriczer são construídos de acordo com o ad quadratum. Embora o
ad triangulum fosse o último método alemão medieval da geometria sagrada,
ele não era facilmente aplicável aos remates e aos arcobotantes que são parte
integrante da construção gótica. Então o ad quadratum foi usado nessas partes essenciais
da estrutura.
A produção do plano
do pináculo era levada a efeito da seguinte maneira:
Röriczer:
"Quereis desenhar um plano para o pináculo segundo a arte dos maçons, por
meio da geometria regular? Deveis então fazer um quadrado, como está aqui designado
pelas letras A:B:C:D; ligar A a B e B a D e D a C e C a A, de modo a obter
uma figura semelhante à do esquema anexo.
Fazer depois um outro
quadrado. Dividir AB em duas partes iguais e chamar E; da mesma maneira,
dividir BD e chamar H; do mesmo modo, dividir DC e chamar F; igualmente,
dividir CA e chamar G. Depois, traçar uma linha de E a H e de H a F, de F
a G e de G a E.
Depois de terdes
assim procedido, fazei outro quadrado sobre este segundo.
Quando terminardes os
três quadrados de tamanho igual a ABCD, IKLM e EHFG, tereis uma figura
semelhante à do esquema anexo.”
Esses três quadrados
exercem uma relação geométrica específica COm um outro: a diagonal do segundo
quadrado é igual ao lado do primeiro quadrado e a diagonal do terceiro é igual
ao lado do segundo. A ação seguinte na geometria de Röriczer envolve o traçado
de quatro cantos; depois, toma-se o raio IN e com um compasso são traçados
quadrantes que produzem as dimensões da moldura côncava do painel e do plano
completo da agulha. A partir desse plano, constrói-se, com a utilização de uma
régua e de um compasso, a planta baixa final de um pináculo.
Com base nessa complexa
planta baixa, a elevação era feita com movimentos igualmente simples de régua e
compasso. Cada um dos maçons que executavam essas obras possuía uma marca individual
que podia ser usada para identificar não só a obra do próprio maçom, mas também
as lojas de que ele provinha. As marcas dos maçons existiram em todos os países
na tradição arquitetural ocidental do Egito antigo em diante e são sigilos
característicos que em geral são derivados geometricamente.
Embora tenha sido um
"segredo maçônico", afirmou-se durante muito tempo que cada loja
central de maçons operativos possuía seu "diagrama matriz" próprio a
partir do qual derivavam todas as marcas utilizadas pelos seus membros. O
Professor Homeyer, em Hof und Hausmarken, publicado em 1870, mencionou que, por
volta do ano de 1820, um certo Dr. Parthey lhe dera um "diagrama matriz"
no qual estavam baseadas todas as marcas dos maçons da Catedral de
Estrasburgo. Diz-se que esse diagrama fora descoberto por um certo Arnold de
Estrasburgo, um arquiteto.
Costuma-se dizer que
em 1828 o maçom Kirchner de Nuremberg estava de posse de um livro que fazia
todas as marcas individuais dos maçons derivarem de uma fonte comum. O
Professor Franz Rziha, em sua obra Studien über Steinmetz-zeichen, publicado em
1883 em Viena, demonstrou que, a partir de determinados diagramas geométricos
fundamentais, poderia ser derivada uma série de "diagramas matrizes"
ou chaves na qual se poderia incluir todas as marcas de maçons conhecidos. Nas
68 lâminas que ilustram essa obra, Rziha enquadrou 1145 marcas em seus próprios
diagramas, demonstrando a universalidade do sistema.
O conhecimento de
todos os níveis da geometria era, assim, uma prerrogativa do franco-maçom. Com
esse conhecimento da geometria das marcas, um maçom podia "provar"
sua marca quando isso fosse exigido dele e também podia julgar a origem de
qualquer outra marca que ele visse. O Professor Rziha descobriu quatro
diagramas geométricos básicos nos quais se baseavam as marcas de todos os
maçons. Os dois primeiros diagramas eram os modelos ad quadratum e ad
triangulum regulares. Os outros dois eram mais complexos, chamados por Rziha de
vierpasse e dreipasse. O vierpasse corresponde à geometria do quadrado que
incorpora vesicas relacionados, ao passo que o dreipasse utilizava uma
combinação diferente de triângulos eqüiláteros e círculos. Cada um desses
diagramas pode ser ampliado à vontade e, então, uma série muito elaborada de figuras
geométricas forma a base das marcas dos maçons.
Rziha descobriu os
"diagramas matrizes" de um grande número dos maiores centros europeus
de conhecimento maçônico, inter alia Nuremberg, Praga, Estrasburgo, Viena,
Colônia e Dresden. A geometria do macrocosmo estava reproduzida até mesmo no
nível mais baixo da tradição maçônica européia e, assim, até mesmo as marcas
mal perceptíveis feitas em pedras isoladas eram, sem dúvida, emblemas das
estruturas transcendentes do universo.
11.
A Geometria Sagrada da Renascença
"Deus
também criou o homem à sua própria imagem: pois, como o mundo é a imagem de
Deus, também o homem é a imagem do mundo.”
H.
Cornelius Agrippa, Filosofia oculta.
Com a redescoberta
dos velhos modos romanos clássicos de arquitetura, a geometria linear
superposicional do período medieval foi rapidamente suplantada por uma
geometria poligonal centralizada. No século XV, na Itália, pode-se ver uma
transição gradual nos pIanos das igrejas da Cruz Latina tradicional para a
centralizada. Essa tendência centralizadora, derivada da prática pagã antiga,
tem sido vista por muitos historiadores como emblema de um movimento de fuga
das crenças cristãs transcendentes da Idade Média para um ethos mais humanista,
antropocêntrico. Essa noção reducionista de que a crença, cristã medieval
mergulhara num ataque furioso de humanismo ateísta exaltado ignora as
correntes subterrâneas do pensamento geométrico do período.
As igrejas
centralizadas colocaram o problema da separação hierárquica da congregação e do
clero e, mais fundamentalmente, a questão do sítio do altar. Os requintes da
geometria centralizada, todavia, estavam crescendo. Uma obra-chave para a
compreensão dessa nova geometria é o primeiro tratado arquitetônico da
Renascença, De re aedificatoria, escrito entre 1443 e 1452 pelo arquiteto
Alberti. As origens pagãs de suas idéias estão mais claramente apresentadas
nos seus desenhos para templos, como ele denomina as igrejas. O círculo, afirma
ele, é a forma primária que, acima de todas as outras, é favorecida pela
natureza, começando-se pela própria forma do mundo. Para os templos, Alberti
demonstra o uso de nove figuras geométricas. Utiliza o círculo, cinco polígonos
regulares (o quadrado, o hexágono, o octógono, o decágono e o dodecágono) e
três retângulos (o quadrado e meio, o quadrado e um terço e o quadrado duplo).
A partir dessas
plantas baixas, Alberti desenvolve anexos geométricos que servem como capelas
laterais. Estas são retangulares ou semicirculares na forma e estão
relacionadas radialmente ao ponto central. Com a adição de figuras
geométricas simples ao poIígono básico ou círculo, pode-se produzir uma
classe quase infinita de configurações.
Alberti inspirou-se
nos edifícios vitruvianos da era clássica, mas, estranhamente, a forma
central que ele mais privilegiou não era co mum nos templos daquele
período. Apenas três templos redondos restaram dos tempos clássicos - o
famoso Panteão e dois pequenos templos peripteriais em Tivoli e em Roma. A
grande maioria dos templos clássicos seguia, naturalmente, um plano
retangular. Toda via, durante a Renascença, outros edifícios poligonais
da antigüidade - como o "templo de Minerva Médica", dodecagonal, em Roma,
na verdade o nymphaeum dos Orti Licianini, e as primeiras estruturas
cristãs, tais como o Santo Stefano Rotondo e Santa Constanza - eram
considerados como templos antigos.
Vitruvio nem mesmo
chegou a incluir edifícios redondos entre as sete classes de templos
enumeradas no seu Terceiro Livro, mas, ao invés, mencionou-os em forma de
apêndice no Livro Quarto ao lado da aberrante forma toscana. Todavia, a
predileção de Alberti pela forma poligonal, influenciada pelos Sólidos
Platônicos, justificava-se com o pretexto de que representava uma volta à
simplicidade litúrgica da Roma de Constantino. Naquele período, o Colégio
Romano de Arquitetos foi compelido a transferir sua perícia do desenho dos
templos para os pagãos à criação de igrejas para a nova fé oficial. O
período constantiniano foi especialmente poderoso para a mentalidade da
Renascença, pois que ele representava o único ponto de fusão da
arquitetura clássica totalmente desenvolvida com a fé pura do Cristianismo
Imperial.
Todavia, na Roma de
Constantino, a forma normal das jgrejas era a basílica, um padrão derivado
dos Tribunais de Lei. Alberti não aprova esse tipo de edifício, mas
menciona de passagem que os cristãos primitivos utilizaram basíIicas
romanas particulares para a celebração dos seus ritos. A basílica, assento
da justiça humana, relacionava-se à religião de maneira simbólica: como se
afirmava que a justiça era um dom de Deus; a presença de Deus está para todo
o sempre na esfera das decisões jurídicas e, por conseguinte, a basílica
foi levada para o reino da adoração.
O plano
fundamentalmente humano e funcional da basílica foi considerado muito prosaico
por Alberti. Ela não desperta no observador um sentimento de reverência e de
piedade, Ela não possui o efeito de purificação que induz um estado de
inocência primal que agrada a Deus porque não foi construída de acordo com a
geometria sagrada. Nas igrejas centralizadas da Renascença, a forma geométrica
é explícita, diferentemente da geometria arcana que subjaz àbasílica ou à
igreja gótica, uma geometria só apreciável pelo iniciado. Num plano da
Renascença, a geometria pura domina esmagadoramente. Cada uma das suas partes
está harmonicamente relacionada, como os membros de um corpo, tornando
manifesta a natureza da divindade.
Como muitos dos seus
contemporâneos, Alberti escreveu extensamente sobre os atributos da igreja
ideal. Como seu tema correlato, a cittá ideale, ou cidade ideal, essa igreja é
uma expressão idealizada do absoluto cósmico, desenhado como uma manifestação
visível da harmonia divina, um conceito essencialmente neoplatônico. Alberti
pretendia que sua igreja fosse construída num terreno elevado, livre em todos
os lados, no centro de uma praça vistosa. Devia ser baseada num plinto elevado
que servia para protegê-Ia contra a profanidade da vida cotidiana e ser
cercada por uma colunada, à maneira dos antigos templos dedicados a Vesta.
Sua geometria
explícita devia ser coberta por um domo vistoso, que devia ser adornado
internamente com caixotões segundo o estilo do Panteão. A abóbada do domo
também devia aparentar semelhança com o céu, na tradição da interpretação
cósmica universal do templo. Assim, como na arquitetura ortodoxa oriental e gótica
ocidental, toda a igreja redonda era um emblema do mundo - a manifestação
criada da Palavra de Deus: um receptáculo perfeito da humanidade.
Como as igrejas
redondas do período dos Templários, essas igrejas centrais não eram vistas
apenas como microcosmos do mundo, mas também como símbolos da universalidade de
Deus. Muitas igrejas centralizadas reviveram inconscientemente o cubo cósmico
na forma de um altar central. O centro, o "uno e absoluto", na iconografia
cristã, é um reflexo d’Aquele que só existe em verdade. Porque sua onipresença
era representada pela realização dos sacramentos, o altar era o centro, o omphalos
para o qual todos os raios do edifício convergiam.
Muitas dessas igrejas
centralizadas foram dedicadas à Virgem Maria. Essa tendência possuía uma razão
simbólica. Desde o período mais antigo da religião cristã, o culto da mãe de
Cristo considerava-a a rainha do céu e a protetora de todo o universo. Essas
idéias surgiram da associação da mitologia com seu sepultamento, sua assunção e
sua coroação, ecoando a coroa circular da rainha celeste a antiquíssima
tradição dos céus circulares.
As igrejas
circulares, todavia, conseguiram um sucesso de curta duração. O maior
número delas foi construído no período de 1490 a 1560. A Cristandade não desistiria
tão facilmente das suas tradições. Em 1483, um artista italiano, Domenico
Neroni, seu patrono Ascanio de VuIterra e um sacerdote anônimo foram
executados por sacrilégio. Inspirados pelo desejo avassalador de conhecer
o Número Perfeito e as proporções que guiavam os escultores antigos na feitura
das efígies dos deuses, eles conceberam um esquema de evocação desses deuses.
Foram sentenciados à morte por realjzarem atos de magia ritual. As proporções
antigas foram tão estreitamente ligadas à religião pagã, que foi só uma
questão de tempo a Igreja rejeitar os "templos" de Alberti
baseados em sua origem pagã. Eventos como este devem ter espalhado as sementes
da dúvida na mente dos ortodoxos.
Em 1554, Pietro
Cataneo, em seu livro I quattro libri di architettura, reiterou o conceito de
que o templo era um símbolo do corpo de Deus. Afirmou que, por essa razão,
as catedrais deviam ser dedicadas a Cristo crucificado e, como tal, deviam
seguir a forma da Cruz Latina. Em 1572, Cado Borromeo, em Instructionum
Fabricae ecclesiasticae et Superlectilis ecclesiasticae, investiu contra a
forma redonda das igrejas afirmando que ela era pagã. Segundo o Concílio de
Trento, ele também recomendou o uso da Cruz Latina.
Embora houvesse
controvérsia e sugestões de heresia em relação ao uso de igrejas redondas, os
sistemas proporcionais antigos eram tidos como admiráveis pelos ortodoxos.
Um documento relativo a S. Francisco della Vigna, em Veneza, fornece-nos um
esclarecimento sobre o sistema proporcional utilizado nas igrejas da Renascença
construídas com formas ortodoxas. O Doge de Veneza, Andrea Gritti, assentara a
pedra fundamental da nova igreja no dia 15 de agosto de 1534 e a
construção foi iniciada sob as ordens de Jacopo Sansovino. Mas, como nas
primeiras dificuldades da Catedral de Milão, surgiram discussões a
respeito do sistema proporcional a ser utilizado. Um entendido em
proporção, Francesco Giorgi, um monge franciscano que publicara em 1525 um
tratado sobre a Harmonia Universal (De Harmonia Mundi Totius), foi encarregado
de escrever um comentário sobre o plano de Sansovino. O tratado de Giorgi
fundira teoria neoplatônica e cristã, o que produziu o efeito de reforçar a
crença já existente na eficácia da razão numérica.
Para essa igreja,
Giorgi sugeriu que a largura da nave tivesse nove passos, já que essa medida é
o quadrado de três. Três é o primeiro número real nos termos pitagóricos
porque tem um começo, um meio e um fim. O comprimento da nave deveria ser três
vezes a largura, o cubo simbólico, 3x3x3, que, como a Cidade da Revelação ou o
Santo dos Santos judaico, contém as consonâncias do Unjverso. A razão entre a
largura e o comprimento, 9:27, também é analisável em termos musicais, formando
um diapason e um diapente (uma oitava e uma quinta). Giorgi, assim, sugeriu a
progressão do lado masculino do triângulo platônico para a nave da igreja.
No lado oriental da
igreja, a capela deveria ter nove passos de largura e seis de comprimento,
representando a cabeça do Homem Vitruviano. No comprimento, essa capela repetia
a largura da nave e, na largura, possuía a razão 2:3, um diapente. O coro,
também, tepetia as dimensões da capela oriental, resultando toda a igreja em
5x9 = 45 passos de comprimento, um disdiapason e um diapente em termos
musicais. As capelas laterais da nave eram largas de três passos, e o
transepto, de se.is passos. A razão da largura das capelas do transepto para
aquela da nave era 4:3, um diatessaron. A altura do teto também mantinha uma
relação de 4: 3 com a largura da nave.
Esse sistema global,
relacionado às proporções ideais do Homem Vitruviano e às harmonias cósmicas de
Platão e Pitágoras, foi recebido com prazer, e até implementado, depois de ter
passado pelo pintor Ticiano, pelo arquiteto Serbio e pelo filósofo humanista
Fortúnio Spira. A fachada da igreja foi completada por Palladio trinta anos
depois, de acordo com o mesmo sistema de proporções e de razões harmônicas.
Palladio foi um dos
maiores expoentes da geometria sagrada da Renascença. Em seus influentes
Quattro libri dell'architettura, Andrea Palladio tentou elaborar um exame geral
de toda a arquitetura. Ele, naturalmente, acentuou seu débito para com Vitrúvio,
e também Alberti. Todavia, foi a Vitrúvio que Palladio deveu sua maior
inspiração. Para ele, Vitrúvio era a chave dos mistérios da arquitetura
antiga, seus sistemas de proporção e seu simbolismo oculto. Mas Palladio não
possuía apenas um conhecimento acadêmico da arquitetura clássica. Ele viajara
por toda a Itália visitando os restos desses edifícios e produzindo esboços
detalhados das medidas a fim de verificar as afirmações vitruvianas.
Palladio escreveu:
"Embora a variedade e as coisas novas agradem a todos, elas não devem ser
executadas ao contrário dos preceitos da arte e ao contrário daquilo que a
razão dita; donde se depreende, que embora os antigos variassem, eles nunca se
afastaram das regras de arte universais e necessárias". Com esse exioma em
mente, Palladio pôs-se a reinterpretar a geometria sagrada clássica antiga no
desenho de seus memoráveis edifícios. As villas de Palladio foram desenhadas
com uma simetria rígida derivada de uma única fórmula geométrica. Os
compartimentos e seus pórticos foram baseados num retângulo dividido por duas
linhas longitudinais e quatro linhas transversais. A sua obra mais famosa,
merecidamente, é a Villa Rotondo, um desenho magistral que gerou muitas imitações
inferiores. Aparentemente, o desenho é mais adequado para um edifício
religioso, já que é óbvia nele uma origem cósmica. Em essência, é composto do
quadrado quartado da terra que suporta o domo circular do céu. Em
todos os edifícios de Palladio, as razões harmônicas são utilizadas no interior
de cada compartimento e na relação de cada compartimento com um outro. A velha
geometria sagrada dos templos pagãos foi refinada num sistema que serviu às
residências palacianas dos ricos.
Palladio exerceu uma
influência profunda sobre a arquitetura da Renascença e mais tarde, na
Inglaterra, Inigo Jones popularizou seu estilo. Em seus Qllattro libri,
Palladio alude a um sistema geral de proporção que utilizou em todas as suas
incumbências. Ele detalha o que considera ser as proporções mais harmoniosas
para as razões largura: comprimento dos compartimentos. Como as igrejas de
AIberti, a obra de PalIadio recomenda as sete formas místicas dos
compartimentos: circular, quadrada, a diagonal do quadrado para o comprimento
do compartimento V2, um quadrado e um terço, um quadrado e meio, um
quadrado e dois terços e o quadrado duplo. As razões recomendadas são as
seguintes: 1; 1:1; V2:1; 3:4; 2:3; 3:5 e 1:2. A terceira é a única que é
incomensurável nessa progressão e é o único número irracional geralmente
encontrado na geometria sagrada da Renascença. Ela aparece em Vitrúvio num sistema
comensurável e, como tal, talvez represente o último vestígio da geometria
sagrada grega antiga, sobrevivente como um fragmento no período romano.
Palladio afirma que
há três grupos diferentes de razões que fornecem boas proporções par.a
compartimentos e dá para cada um deles um modo de cálculo das alturas
baseado num método geométrico e aritmético. Supondo-se que um compartimento
meça 6x 12 pés (o quadrado duplo), a sua altura deverá ser de 9 pés. Se ele
medir 4x9 pés, sua altura deverá ser de 6 pés. No método aritmético, o segundo
termo excede o primeiro na mesma medida em que o terceiro excede o segundo. No
método geométrico, o primeiro está para o segundo termo assim como o segundo
está para o terceiro. Um outro exemplo, mais complexo, é fornecido: o método
harmônico.
Para um compartimento
de 6x12, a altura, pelo método harmônico, será de 8 pés. Esse método
geométrico estava de acordo com a idéia dos harmônicos exposta no Timeu de
Platão como "a média excedendo um extremo e sendo excedida pelo outro pela
mesma fração dos extremos". Na progressão 6:8:12, a média 8 excede 6 em 1/3
de 6 e é excedida por 12 em 1/3 de 12.
Talvez Palladio
tivesse extraído essa idéia diretamente das obras de Alberti, mas ela também
fora tratada por Giorgi em seu Harmonia Mundi e por Ficino em seu comentário
sobre o Timeu. Ela está baseada, naturalmente, na teoria musical clássica e,
como tal, provém diretamente da Harmonia das Esferas, a pulsação mística do Universo
reconhecida igualmente por pagãos e por mágicos. Essa idéia é comum à
Renascença e ao período medieval, mas foi durante esse último período que ela
foi formalizada no comentário de Ficino e em obras como De Musica, de Boécio.
Considerava-se que o
uso, na arquitetura, de harmonias derivadas musicalmente era uma expressão da
Harmonia Divina engendrada no ato de criação por Deus; em termos modernos, o
"eco" da Grande Explosão que deu início ao Universo. Por meio dessa
expressividade da Harmonia Divina, estavam integrados os símbolos duais do
templo como o corpo do Homem, o microcosmo, e o templo como incorporação da
totalidade da criação. Em De Sculptura, publicado em 1503, o autor Pomponius
Gauricus formula a seguinte questão: "Que geômetra, que músico foi esse
que formou o homem dessa maneira?" Gauricus, novamente, baseou amplamente
as suas teorias no Timeu de Platão.
A conexão explícita
entre as proporções visuais e audíveis na Renascença traz novamente à baila a
possibilidade de que ela possa ter sido derivada inicialmente da necessidade de
se construir os templos como instrumentos que pudessem canalizar as energias
telúricas. No pensamento pitagórico-platônico, a própria música era vista como
uma expressão da Harmonia Universal e era parte essencial da formação de um
arquiteto. Os grandes arquitetos da Renascença de Brunelleschi em diante
estudaram avidamente a música dos antigos. As aberrações arquitetônicas eram
vistas em termos de discordância musical e essas alterações do sistema de
proporção significariam que o templo não podia mais agir como um instrumento
para a produção da Harmonia Divina. Por exemplo, durante a construção da
igreja de S. Francisco, em Rimini, Alberti preveniu Matteo de Pasti de que a
alteração das proporções das pilastras "destruiria todas as relações
musicais".
Escritores como
Lomazzo referem-se constantemente ao corpo humano em termos de harmonia
musical. Por exemplo, a distância entre o nariz e o queixo e entre o queixo e o
encontro das clavículas é um diapason, Lomazzo, em seu Idea del Tempio della
Pittura, publicado em 1590, afirma que mestres como Leonardo, Miguel Ângelo e
Ferrari chegaram ao uso da proporção harmônica por meio do estudo da música.
Lomazzo menciona como o arquiteto Giacomo Soldati acrescentou às três ordens
gregas e às duas romanas uma sexta, que chamou de Ordem Harmônica. Soldati era
um engenheiro que estava envolvido principalmente com a construção de máquinas
hidráulicas e, assim, era adepto da utilização do conhecimento geométrico
necessário à criação de uma sexta ordem de arquitetura. Infelizmente, não
sobreviveu nenhum desenho dessa sexta ordem, nem existe edifício algum
construído nesse estilo. Todavia, pretendia-se que a sexta ordem deveria conter
todas as qualidades inerentes às cinco ordens originais e expressar mais
vigorosamente a unidade básica e os padrões harmônicos do Universo.
Acreditava-se que a
sexta ordem fosse a recriação da ordem perdida do Templo de Jerusalém, que foi
inspirada diretamente por Jeová quando ordenou a Salomão que o construísse
segundo medidas preordenadas. As alegações pagãs dos ortodoxos foram silenciadas.
A ortodoxia total do Templo de Salomão, ordenada diretamente por Deus, foi o
precedente para a aplicação das razões harmônicas da geometria sagrada nos
edifícios cristãos. A reconstrução do Templo tantas vezes destruído também se
tornou o objetivo de muitos arquitetos desse período. Como Soldati, o jesuíta
espanhol Villalpanda estava interessado na recuperação da sexta ordem. Suas
pesquisas levaram a uma nova geração do desenho.
Talvez a mais
impressionante e complexa obra dentre aquelas que foram ocasionadas pelas teorias
a respeito do Templo de Jerusalém tenha sido El Escorial, o estupendo
palácio-mosteiro erigido sob as ordens de Felipe II de Espanha. A fundação do
Mosteiro de San Lorenzo de El Escorial, para dar seu nome completo, foi concebida
como um ato de ação de graças pela vitória espanhola na batalha de San Quentin.
EI Escorial foi
construído como um resultado direto de um voto sagrado que Felipe II fez na
véspera da batalha. Travada no dia de São Lourenço, a 10 de agosto de 1557, a
batalha resultou na derrota dos franceses pelas forças de Felipe. Em
reconhecimento desse dia momentoso, o eixo da igreja, e por conseguinte todo o
padrão geométrico do mosteiro, foi orientado para o ponto do pôr-do-sol a 10
de agosto. Esse procedimento era extremamente incomum, pois o nascer-do-sol
era e é universalmente reconhecido como o horário correto para a determinação
de tais alinhamentos.
Diz-se que o plano
geral do edifício, na forma de uma grelha, lembra o martírio apavorante do
santo padroeiro, de quem o rei era um devoto. Felipe decidiu construir esse
grande estabelecimento monástico para a Ordem Hieronimita e o planejou de
acordo com revelações bíblicas. A obra de construção foi iniciada a 23 de abril
de 1563 e completada 21 anos depois. O arquiteto Juan Bautista de Toledo foi
encarregado de dirigir a obra, mas, com sua morte prematura, seu assistente
Juan de Herrera levou-a adiante e completou com êxito um magnífico edifício
sagrado num estilo muito pessoal. Não obstante, a despeito da sua marca
pessoal, os princípios seguiam estritamente os preceitos canônicos. Felipe II e
Juan Herrera eram seguidores ardorosos do místico espanhol Ramón Lull, cujas
exposições matemáticas da Harmonia Universal lhe haviam conseguido a pena de
morte por heresia anti-islâmica durante a ocupação moura.
Herrera aplicara
anteriormente as harmonias derivadas musicalmente em sua construção da
catedral de Valladolid e pretendeu fazer o mesmo com o Escorial. Basicamente
vitruviana em desenho, a geometria é a do ad triangulum. Toda a planta baixa
abrange o Homem Vitruviano. No planejamento global, o Escorial ecoa o Campo dos
Israelitas, um tema abordado por Villalpanda em seu tratado erudito sobre
Ezequiel. Como a imagem do microcosmo, o mosteiro foi fundado num dia
astrológica e historicamente favorável e desde o princípio pretendeu-se que ele
seria o epítome de todas as artes e letras da época.
O ambiente dos
círculos místicos espanhóis da época da fundação do Escorial produziram uma
obra monumental, In Ezechielem Explanationes. Embora fosse publicada após o
completamento do mosteiro, ela fornece a chave das idéias inextricavelmente
envolvidas na obra. Dois jesuítas, Juan Bautista Villalpanda e Jeronimo Prado,
puseram em prática durante longo tempo uma série de pesquisas complexas e esmeradas
sobre a estrutura e o simbolismo do Templo de Salomão e a sua interpretação na
visão de Ezequiel. A reconstrução, e o raciocínio que está por trás dela, ocupa
a maior parte do segundo dos três tomos que comentam o Livro de Ezequiel. Estes
livros foram financiados por Felipe lI, a quem foi dedicado o primeiro volume.
A dedicatória diz que ele "parecia (...) Salomão na grandeza de alma e de
sabedoria enquanto construía a mais magnífica e verdadeira das obras reais, San
Lorenzo de el Escorial". Esta similaridade imaginosa com Salomão ecoa as
mesmíssimas alusões aplicadas ao Imperador Romano Oriental Justiniano e ao
Santo Imperador Romano Carlos Magno. Codimus relata que Justiniano, ao ver a
grande igreja de Santa Sofia em Constantinopla, exclamou "Salomão, eu o
excedi!" e Carlos Magno, segundo seu biógrafo Notker, o Gago, construiu
as suas igrejas e seus palácios "seguindo o exemplo de Salomão". Além
disso, um dos títulos ganhos por Felipe II era Rei de Jerusalém e o Escorial
foi modelado segundo o templo dessa cidade.
De acordo com
VilIalpanda, a harmonia platônica utilizada por AIberti, PalIadio e Soldati
fora revelada a Salomão por Deus. O sistema emprega as harmonias musicais do
diatessaron, do diapason, do diapente, do diapason com diapente e do disdiapason;
mas rejeita a sexta consonância vitruviana do diapason com diatessaron. Por
estes meios era a relacão complexa dos elementos da arquitetura clássica
relacionada à Vontade de Deus.
Esta vasta obra
mística foi lida por um amplíssimo número de pessoas e exerceu uma influência
muito grande, pois que sintetizava os mistérios escatológicos do Velho
Testamento com as teorias grecoromanas platônicas de Vitrúvio. Herrera, o
arquiteto tão intimamente ligado à execução dos desejos de Felipe II, é
apontado por VilIalpanda como seu mestre. Como um discípulo de Herrera,
Villalpanda estava na posição perfeita para expor os princípios ocultos do Escorial
e seu predecessor, o Templo salomônico. Sua reconstituição pode ser situada em
1580, dezesseis anos antes da publicação, e Herrera, ao ver os desenhos, teria
comentado que um edifício de tal beleza só poderia provir de Deus.
Villalpanda e Prado
não foram os primeiros comentadores a tentar uma reconstrução perfeita do
Templo salomônico. Na verdade, o primeiro e talvez mais famoso bibliotecário
do Escorial, Benito Arias Montano, publicara em 1572 a sua própria
interpretação do Templo. O seu plano era todo em estilo clássico com uma torre
de quatro estágios à maneira da Renascença. Villalpanda desprezou esse plano
como uma fantasia porque "não seguia a especificação da santa profecia,
nem mesmo em parte". VilIalpanda, um grande acadêmico versado na Bíblia e
um hebraísta, acreditava que ele, através dos exercícios espirituais de sua
ordem, chegara à verdadeira manifestação do Templo. Suas raízes místicas, na
verdade ocultas, estavam na Cabala hebraica, o cânone pagão de Vitrúvio, e no
misticismo matemático do herético Ramón Lull.
Os recintos do
templo, freqüentemente ignorados pelos reconstrutores posteriores, especialmente
aqueles de credo protestante, foram sumamente importantes para Villalpanda. Executadas
com a forma geral de um quadrado, as sete cortes representavam astrologicamente
os sete planetas e outros pontos significativos, as casas astrológicas e as
tribos de Israel.
Nem todos os
edifícios místicos do período voltavam às fontes bíblicas para dali retirarem
sua inspiração. Um edifício único na Inglaterra, que exibe publicamente a
geometria sagrada e a matemática oculta, é a famosa Loja Triangular, em
Rushton, no Northamptonshire. Esse edifício devocional foi erigido sob as
ordem de Sir Tomas Tresham, um devoto do catolicismo romano que desejou
continuar sua adoração particular num clima político hostil àquela religião. A
Loja Triangular era a sua expressão de sua devoção à Santíssima Trindade, e,
sendo um emblema da Trindade, foi construída na forma de um triângulo
eqüilátero.
Cada um dos lados da
loja tem um comprimento de 33 pés e 4 polegadas. Há três pavimentos; três
janelas em cada andar em cada um dos três lados e cada janela divide-se em
três. Há três inscrições latinas, cada uma das quais tem 33 letras. Uma delas,
todavia, é o símbolo &, o que perfaz a centena redonda notável no
comprimento total dos lados. O teto foi terminado com três frontões de cada
lado, e um remate de três lados foi executado acima do teto. Abaixo das janelas
do segundo andar, no lado da entrada. há a data 1593 e as iniciais do construtor,
T. T. Mesmo a letra "T” é símbolo do três.
O ornameqto, se assim
se pode chamar, está profundamente ocultado no volume. Num frontão há as
figuras 3898 e abaixo delas
a Menorah, o
candelabro de sete ramos dos judeus. No frontão seguinte, há a inscrição
Respicite e um relógio solar. No tercejro frontão está o número 3509 e a pedra
de sete olhos. Cada um dos três lados representa, assim, um aspecto da Trindade.
A loja continua sendo
uma singularidade, embora uma igreja triangular emblemática da Santíssima
Trindade tenha sido erigida em Bermondsey, em Londres, em 1962. Os
edifícios triangulares são notoriamente desprovidos de praticidade na
acomodação de fiéis e poucos foram construídos dessa maneira. A geometria
sagrada faz concessões a esse respeito e capacita o arquiteto a incorporar o simbolismo
numa maneira arcana. Tresham ultrapassou o método tradicional e cometeu uma
"loucura" memorável - que continua sendo um testemunho de um
extraordinário fervor religioso.
Mais ou menos no
mesmo período, a magia, despojada de seu rótulo herético e praticada sob a nova
ordem do Rosacrucianismo, começou a florescer abertamente na Inglaterra
protestante e polímatos como John Dee e Robert Fludd, cujas pesquisas iam da
matemátjca à alquimia, via astrologia e ocultismo, criaram vários sistemas de
geometria sagrada que codificavam suas descobertas mágicas.
12. A
Geometria do Barroco
Aplica-se o termo
barroco hoje em dia à arquitetura dos séculos XVII e XVIII, tendo sido
originalmente um pejorativo derivado da palavra italiana baroco. Essa palavra
foi usada pelos filósofos da Idade Média para descrever qualquer idéia por
demais complexa ou qualquer conceito intrincado. Também se aplicava a algo
bizarro ou disforme, por exemplo uma pérola, e pressupunha a quebra das regras
canônicas da proporção ao capricho do artista ou arquiteto. Assim, o Barroco, como
o movimento Art Nouveau posterior, era visto pelos puristas como degenerado por
causa do seu ponto de partida mais ou menos distanciado do cânone rígido da
arquitetura clássica.
A arquitetura barroca
pode ser vista como uma continuação da revitalização clássica da Renascença. Na
verdade, os primeiros edifícios em estilo barroco enquadram-se perfeitamente na
tradição e podem ser distinguidos apenas por diferenças de detalhe na manipulação
do ornamento. Todavia, o Barroco propriamente dito rompe com o estilo
recomendado da arquitetura romana e este fato está refletido em sua geometria
subjacente.
Afirma-se amiúde
erroneamente que na geometria sagrada clássica as formas dos edifícios devem
ser relacionadas simplesmente às figuras geométricas principais. No Barroco
vemos a primeira evasão deste conceito, pois, embora as formas se relacionem às
figuras geométricas familiares, elas devem estar relacionadas a um ou dois intervalos.
Assim, uma forma comum nos interiores da igreja barroca é o oval. Essa forma,
como seus precursores espirituais na era megalítica, pode ser baseada em
figuras significativas como o triângulo 3:4:5 pitagórico. Ao passo que as
fachadas das igrejas e das catedrais barrocas ainda utilizavam combinações de
retângulos de raiz, as plantas baixas aumentavam o número de liberdades.
Os edifícios de
Gianlorenzo Bernini demonstram admiravelmente as complexidades da geometria
sagrada barroca. Seu S. Andrea al Quirinale, em Roma, construído como uma
igreja para noviços jesuítas, entre 1658 e 1670, era um oval transverso de
setenta pés por quarenta, em desafio deliberado à orientação tradicional
do altar ao longo do eixo. Desse oval emergem oito capelas laterais que, com
o nicho ocupado pelo altar elevado e pela entrada no lado oposto, fornecem uma geometria
décupla. Nunca antes fora tentado um plano como este, que não tem paralelo em
termos geométricos. Muitos anos antes, o excêntrico arquiteto sagrado Francesco
Borromini construíra igrejas segundo um sistema ad triangulum modificado.
Embora tenha sido feita uma breve tentativa, durante a construção da Catedral
de Milão, de se usar o ad triangulum, o sistema era extremamente incomum na
Itália antes do século XVII. Talvez a SS Trinita, de Vitozzi, em Turim, seja o
único exemplo mais antigo, e só foi iniciada em 1598.
O desenho sem dúvida
alguma barroco de Borromini para o Archiginnasio, depois sede da Universidade
de Roma e mais tarde ainda dos Arquivos Estatais Italianos, incorporou a
pequena igreja de Santo Ivo. Ela fora desenhada segundo o plano do Selo de Salomão,
dois triângulos interpenetrantes. A planta baixa está embelezada pelo
desenvolvimento de vértices alternados do selo em recôncavos semicirculares
simples e pelo fechamento dos outros a meio caminho por traços convexos.
Paredes convexas e côncavas inte ragem, assim, com pequenas paredes
intersticiais retas para produzirem um interior ondulante que, não obstante,
limita-se rigidamente à geometria sagrada.
Externamente, Santo
Ivo ecoa o hexágono do interior. Uma cúpula encimada por seis arcobotantes
eleva-se para um remate central que é uma espiral antidextrorsa de três voltas
e meia, um eco dos zigurates antigos da Babilônia. Na verdade, muitas
ilustrações contemporâneas da Torre de BabeI apresentam essa forma espiral.
As três voltas e meia
do remate espiral têm paralelo no número de voltas da serpente interna
Kundalini do Budismo Tântrico indiano. Borromini aqui passa um recibo do
conhecimento arcano manipulado de maneira verdadeiramente moderna.
Na atmosfera
conservadora de Roma, a visão genuinamente barroca de Borromini recebeu poucos
aplausos. Diferentemente da arquitetura em voga, suas obras baseavam-se mais na
pura forma geométrica do que no Homem Vitruviano. Bernini criticou-o, chamando
sua arquitetura de extravagante, pois, ao passo que outros arquitetos usavam a
estrutura humana como ponto de partida, Borromini baseou seus edifícios na
fantasia. Utilizar uma geometria in comum era considerado heresia, pois
ela envolvia princípios e conceitos externos à fé cristã. Afinal, não fazia
muito tempo que Giordano Bruno fora queimado na fogueira por heresia (1600).
Sua idéia neoplatônica do universo como um todo harmonioso era mais ou menos
aceitável na Renascença católica, mas as idéias neopagãs expressas em sua
geometria não o eram. Ele utilizara explicitamente diagramas geométricos para
expressar os atributos de Deus, figuras microscópicas para uma compreensão do
macrocosmo.
A influência de
Borromini, todavia, não foi abafada. Seu sucessor natural foi Guarino Guarini,
que desenhou a singular S. Lorenzo e a Cappella della S. Sindone em Turim.
Esses edifícios seguem Borromini na sua utilização usual do ornamento e do
esboço. San Lorenzo foi desenhada como um octograma com uma série de suportes
de domo que são uma reminiscência de uma prática antiga, como a Grande Mesquita
de C6rdova, na Espanha (875). Este padrão octogrâmico, inscrito num quadrado,
serviu para a "nave" da igreja, ao passo que um oval formou o
santuário. Todavia, como a obra de Borromini, esse oval mascarou um Selo de Salomão,
em cujo centro ficava o altar principal.
Outra obra-prima de
Guarini foi a capela que ele desenhou para a guarda daquela que talvez seja a
mais santa e certamente a mais contenciosa relíquia da Cristandade - o sudário
de Turim. Colocada entre o coro da velha catedral e o palácio real, essa
capela foi concebida como uma estrutura cilíndrica encimada por um domo ad
triangulum modificado. Esse ad triangulum não era verdadeiramente reto, pois
continha outra singularidade barroca, uma simetria nônupla. Construído, o corpo
da capela tem uma simetria nônupla que se reduz a uma simetria tripla no nível
do arco. Este, por sua vez, compõe a abóbada. No centro dela há uma estrela de
doze pontas. No todo, a abóbada consiste de 36 arcos e 72 janelas, fato que enfatiza
o simbolismo duodécuplo.
A palavra barroco
tende a evocar na mente de muitas pessoas uma disposição desenfreada de
ornamento aparentemente casual que se mantém suspensa, como que por mágica, de
uma tela de fundo de motivos clássicos desconectados arranjados de maneira
teatralmente espetacular. As igrejas da Europa central, reconstruídas à maneira
barroca após a Guerra dos Trinta Anos, favorecem a formação dessa imagem.
Igrejas como a de Sváty Mikulas em Praga ou a igreja de peregrinação de Vierzehnheiligen
na Alemanha talvez sejam exemplos típicos das melhores dessas igrejas. Ambas
possuem exteriores retilíneos que ocultam interiores extremamente curvos.
Uma série de vesicas, círculos e ovais está perfeitamente articulada a uma
estrutura de retângulos.
Em Vierzehnheiligen,
o arquiteto Balthasar Neumann executou uma planta baixa totalmente independente
do plano da abóbada, combinando, assim, duas geometrias diferentes mas
superpostas. Os princípios da geometria sagrada que guiavam os arquitetos da
Renascença foram modificados e remodificados até que a geometria do edifício
fosse modificada por uma pletora de geometrias terciárias e quaternárias. Na
Inglaterra, todavia, as velhas tradições foram mantidas até uma data bastante
posterior.
Sir Christopher Wren
talvez seja o arquiteto inglês mais famoso de todos os tempos. Só ele, entre os
arquitetos, é mencionado nas histórias correntes e suas obras-primas, em
Oxford, Cambridge e Londres, são admiradas anualmente por milhares de turistas
que, de outra maneira, não costumam se interessar por arquitetos. Wren foi um
cientista que chegou à arquitetura por um ponto de vista racionalista. Seu
mentor espiritual foi naturalmente o ubíquo Vitrúvio, mas Wren utilizou seus
princípios apenas como pontos de partida que ele simplificou. Quando lecionava
em Oxford, em 1657, pronunciou uma conferência em que expôs seu ethos:
"As
Demonstrações Mntemáticas, constituindo-se sobre as inexpugnáveis Fundações da
Geometria e da Aritmética, são as únicas Verdades que podem mergulhar na Mente
do Homem. vazia de toda Incerteza; e todos os outros Discursos participam mais
ou menos da Verdade, segundo seus Assuntos sejam mais ou menos capazes de
Demonstração Matemática.”
Assim, para Wren, a
geometria era a pedra de toque, a base infalível e imutável contra a qual todo
conhecimento deve ser julgado. Seus escritos teóricos são poucos, pois os
arquitetos ingleses não tendiam a um autojulgamento nessas práticas,
diferentemente de suas contrapartidas italianas. Todavia, em Parentalia,
escrito pelo filho de Wren, há um apêndice composto de quatro Tracts, "(...)
Bosquejos grosseiros, imperfeitos (...)" que, embora sejam notas fragmentárias,
esclarecem a prática da geometria sagrada na Inglaterra do século XVII.
O Tract I discute as
intenções da arquitetura, que "visa a Eternidade". A disciplina da
arquitetura é idealmente eterna e, portanto, baseia-se nas Ordens Clássicas que
são "a única Coisa incapaz de Modos e de Modas", e, como tal,
representam a verdadeira beleza canônica, com uma base estética fundada na
geometria.
De acordo com Wren,
há duas causas de beleza, a natural e a convencional. A beleza natural deriva
diretamente da geometria e as figuras geométricas concordam com a "Lei da
Natureza" para formarem o mais belo. A beleza convencional baseia-se na
associação e, conseqüentemente, é inferior àquela que deriva geometricamente.
Nas suas igrejas da
Cidade de Londres, e na obra-prima da Catedral de São Paulo, a geometria pode
ser vista como o princípio condutor. Este fato se evidencia ainda mais no caso
de muitos campanários de igrejas da City, que são pouco mais do que uma pilha
de elementos geométricos. Isso não lhes tira o mérito de maneira alguma, pois
cada elemento foi magistralmente combinado com o que está abaixo dele, criando
estruturas barrocas ao mesmo tempo elegantes e exóticas. Mesmo o domo de São
Paulo pode ser reduzido geometricamente a Mma "pilha de elementos"
comparável a um Chorten tibetano e pode merecer uma interpretação simbólica
similar.
Embora o nome da Catedral
de São Paulo evoque agora visões de uma obra-prima barroca, antes do Grande
Incêndio de Londres em 1666 ela era uma das maiores igrejas medievais da Europa.
Erguida sobre as fundações de uma igreja mais antiga, essa obra-prima gótica
possuía a torre mais alta da Inglaterra. Com 555 pés, a torre era a estrutura
mais alta jamais construída em Londres até a construção da Torre dos Correios
em 1965. A torre desapareceu num incêndio no século XVI e a catedral gótica foi
irremediavelmente prejudicada num desastre que incinerou grande parte da cidade.
A reconstrução da
catedral foi discutida pelo "Vitruvius Brittanicus", Inigo Jones,
Arquiteto da Corte, nos anos 1530. Seus planos nunca foram executados. Mesmo
depois do Grande Incêndio, os restos foram arranjados às pressas para
utilização posterior, mas por volta de 1672, quando as paredes inclinadas e a
pedra de cantaria desintegrada ameaçavam transformar a congregação numa
avalanche de pedregulhos, a catedral foi fechada. 'Wren, que fora indicado anteriormente
como o arquiteto encarregado da construção, aceitou a oportunidade de edificar
uma nova catedral.
Após muitos planos e
modelos, a catedral final emergiu. Baseada no ad quadratum gótico, o desenho
desenvolveu-se de uma estrutura centralizada albertiana. para um plano
tradicional, com nave, naves laterais, transeptos e grande coro. Todavia, foi
mantida a característica principal, um espaço central no cruzamento. Geometricamente,
as partes da catedral foram desenhadas predominantemente de acordo com a razão
3:2:1, embora a razão 2: 1 também seja comum. Assim, a nave tem 41 pés de
largura e 82 pés de altura; as naves laterais possuem 19x38 pés; o espaço
abaixo do domo possui 108 pés de largura e 216 de altura; e as janelas medem
12x24 pés. A geometria básica da planta baixa de todo o edifício foi desenhada
no interior de um quadrado duplo de 250x500 pés. Essa construção nacional tem
as mesmas proporções dos templos da Pirâmide de Escada, do Tabernáculo
Hebraico e do Templo de Salomão, pontos que não foram perdidos pelos
franco-maçons operativos liderados por Thomas Strong, a quem Wren empregou para
construir seu magnum opus.
A altura global da
catedral também aderiu a dimensões místicas, possuindo 365 pés desde o nível do
chão até o topo da cruz dourada que encima o vasto domo. Esse número, o número
dos dias do ano solar, representa a consumação do ano de Deus, o Tempo Cósmico
em que o Reino do Céu se cumpre na Terra. Essa altura de 365 pés foi utilizada
nos anos 1930 na catedral anglicana de Guildford, onde Sir Edward Maufe
incorporou essa medida ao esquema ad triangulum. Além das suas conotações
anuais, o número 365 equivale em gematria ao nome Abraxas, que, além de ser a
origem da palavra mágica Abracadabra, simboliza a consumação de todo conhecimento.
Mais importante que isso, a figura 365 pés é uma medida geodésica, ligada
diretamente às dimensões do planeta. É a milésima parte da extensão ao nível do
chão de um grau da latitude em Londres, que é de 365.000 pés. 'Wren, que
certa vez medira o globo da Lua para seu patrono o rei Carlos II, não
usaria casualmente essa medida.
13. A
Geometria Sagrada no Exílio
Embora após a época
de Wren e Newton houvesse um novo mundo secular em construção, durante o século
XVlII havia ainda um interesse pelas máximas da harmonia musical de Palladio na
construção. Em 1736 surgiu o livro de Robert Morris, intitulado Lectures on
Architecture, consisting of rules founded upon Harmonick and Arithmetical
Proportions in Building. As idéias expostas nesta obra seguiam a teoria de que,
exatamente como existem apenas sete graus na música que podem ser discernidos
pelo ouvido humano, assim também existem apenas sete formas compostas de cubos
apropriadas à elegância e à beleza.
De acordo com Morris,
1:1:1 era o cubo perfeito; 1 1/2:1:1 o cubo e meio; 2:1:1 dois cubos colocados
lado a lado; 3:2:1 seis cubos perfeitos; 5:4:3 sessenta cubos e 6:4:3 setenta e
dois cubos. As proporções harmônicas consistentes que são visíveis hoje em muitas
casas georgianas atestam seu poder sobre as mentes de muitos arquitetos
seculares especulativos do século XVIII. Todavia, por mais imperfeita que sua
interpretação da geometria sagrada possa ter parecido ser, esses arquitetos
ainda reconheciam que, para se criar harmonia, deve-se começar com uma
estrutura geométrica sobre a qual se deve preparar um desenho.
No século XIX, muitas
das idéias dos séculos anteriores ha viam sido rebaixadas a uma mera
cópia. Os únicos arquitetos que trabalharam com forças reais foram os
engenheiros civis, tais como Thomas Telford e Isambard Brunel, e mais tarde
Gustave Eiffel e Louis Sullivan, que produziram edifícios e estruturas
cujas proporções foram exigidas pelas restrições da engenharia. Seus
contemporâneos, nesse ínterim, contentaram-se em geral em desenvolver cópias
servis de estilo mourisco, gótico, romântico, bizantino, palladiano, paladano,
neo-renascentista, ou, pior, misturas e sínteses bizarras desses estilos. As
melhores dessas misturas figuram hoje como maravilhosos monumentos
idiossincráticos, os predecessores espirituais da Disneylândia. As piores
sucumbiram há muito tempo ao martelo do demolidor.
A arquitetura sagrada
do século passado foi principalmente imitativa. Pilhas enormes, como o Sacré
Coeur de Paris, erigido para comemorar o esmagamento da Comuna anarquista de
1875, incorporaram a geometria, mas, como as igrejas "decoradas" em
todos os detalhes, como as de Pugin, pouco tiveram de místico em seu planejamento.
A pesquisa sobre esses assuntos é insuficiente. Todavia, pode-se dizer com alguma
certeza que um grande número de igrejas que brotaram entre o proletariado
urbano foi desenhado simplesmente como exercícios. Cidades como Swindon e
Crewe, dormitórios para funcionários explorados de rodovias, foram erigidas com
o mínimo de custo e de planejamento, e assim também o foram seus templos
espirituais.
No outro lado da
moeda, no reino do verdadeiramente oculto, o século XIX foi algo como uma
renascença. Livre do temor da inquisição, tendo o poder da igreja sido quebrado
pela revolução política e por brechas científicas, os praticantes das velhas
ciências ocultas puderam sair à luz e expôr suas teorias e suas descobertas.
Surgiu um grande interesse pela astrologia, pelo espiritualismo e por todas
as espécies de magia. Necromantes como o mago francês Éliphas Levi puseram em
prática evocações dos espíritos dos mortos - e publicaram livros com os seus
resultados. Na sua magnífica obra Transcendental Magic, It’s Doctrine and
Ritual, ele descreve em detalhe a evocação do espírito de Apolônio de Tyana,
o grande milagreiro pagão da antigüidade. Neste ato, o sinal do pentagrama foi
escavado sobre o mármore branco de um altar trazido especialmente com esse
objetivo. Depois de vários ritos, um ser foi conjurado, mas a magia de Lévi não
pôde controlar esse espírito e ele se perdeu.
Uma tal descrição de
uma operação mágica não poderia ter sido publicada antes do século XIX. Era tal
a falta de fé no poder da Cristandade, que muitas idéias "frescas"
foram postas em circulação. Muitos desses conceitos provieram do conhecimento
antigo. Na arquitetura, muitos segredos maçônicos e geomânticos antigos foram
dívulgados em 1892 com a publicação de Architecture, Mysticism and Myth, de W.
R. Lethaby. Cinco anos depois, William Stirling publicou anonimamente sua obra-prima
incomparável, The Canon, que expôs as conexões entre a arquitetura dos antigos
e a revelação mágica e escritural. Pela primeira vez na história muitos
mistérios ocultos foram publicados de maneira facilmente compreensível. Os segredos
maçônicos, que durante muitos anos haviam vazado aos poucos em vários livros,
foram pela primeira vez amalgamados com o conhecimento diversificado que então
era colhido dos quatro cantos do mundo por antropólogos e folcloristas.
The Secret Doctrine e
Isis Unveiled, livros de Madame Blavatsky, trouxeram muito conhecimento
esotérico oriental e egípcio para uma forma facilmente consumível pela mente
ocidental. Na verdade, a influência do seu pensamento "teosófico"
exerceu uma profunda influência sobre o século XIX, desde os escritos e
arquitetura de Rudolf Steiner até os edifícios modernos do grupo De Stijl e até
mesmo, por meio da doutrina das raças originais, às teorias racistas dos
nazistas alemães. A Ordem ocultista da Aurora Dourada e os seus muitos grupos
paralelos também tomaram disponível muito do conhecimento metafísico arcano
dos mágicos antigos e medievais. Combinados com essa grande revitalização do
conhecimento oculto, os grandes progressos em ciência e tecnologia apresentados
nos séculos XIX e XX tornaram possível investigar a estrutura física subjacente da
matéria e da geometria orgânica dos reinos vegetal e mineral.
Todavia, o leitor
verá que estamos numa época materialista, de maneira que, embora esses
princípios arcanos tenham sido publicados, sua aplicação à vida cotidiana foi e
é feita de maneira velada. Os princípios da geometria sagrada, não obstante
sejam muito bem conhecidos a essa altura, carregam consigo o poder antigo e sua aplicação
ainda produz o efeito desejado. Todavia, essa crença infelizmente tem hoje o
interesse de apenas uma minoria. A maioria das pessoas a ignora; na verdade,
sua recíproca também é verdadeira.
No começo do século
XX, o culto da iluminação tornara impossível a um arquiteto admitir que ele
estava trabalhando segundo princípios esotéricos. Assim como a geomancia fora
em grande medida extirpada, e por toda a parte da superfície da Terra fosse
considerada igualmente profana, assim também a geometria sagrada foi vista
apenas como uma aderência supersticiosa a um sistema sem valor algum para a
tradição. De fato, as coisas foram ainda mais longe. A maioria dos
arquitetos não estava consciente de que havia uma tradição.
Um livro típico do
período, Hints on Building a Church, de Henry Parr Maskell (1905), apresenta um
guia muito insuficiente das medidas canônicas. Seu conhecimento da geometria
sagrada era mínimo, mas conseguiu escrever uma obra influente sobre construção
de igrejas. Por volta de 1905, só os arquitetos versados no saber maçônico
antigo, ou, de fato, os franco-maçons praticantes, estavam interessados nas
sutilezas da geometria canônica. Muito do interesse passou para teóricos
arquiteturais acadêmicos, como Lethaby.
Maskell escreveu:
"Nossos predecessores acreditavam muito naquilo que a psicologia moderna chama
de mente subconsciente. (...) O 'sentido interno' fazia todas as avaliações
inconscientemente. Devemos reconhecer que essa crença era justificada, via de
regra, em suas obras, mesmo nos assuntos mais abstrusos da acústica e da
ventilação". Esta afirmação, naturalmente, não faz sentido. Não se erige
por meios "inconscientes" uma catedral como a de Salisbury. com uma
torre de quatrocentos pés que resistiu por setecentos anos. Edifícios como esse
são o resultado de uma avançada tecnologia de arquitetura, planejados de acordo
com os princípios seguros da geometria. Por volta do começo deste século, a
idéia de progresso. demonstrada tão convincentemente por avanços tecnológicos
como as telecomunicações, a luz elétrica e os veículos a motor, tornou impossível
o fato de que os construtores da Idade Média tivessem possuído planejamentos
inteligentes. As plantas de execução dos arquitetos medievais repousam
esquecIdas nas bibliotecas das catedrais. de maneira que a teoria "do
inconsciente" era uma desculpa conveniente.
As idéias
psicológicas de escritores como Maskell devem ter sido condicionadas pela obra
recente de psicólogos como C. G. Jung. Em sua obra mais antiga, Jung
discute as fantasias experimentadas por um médium histérico que ele estudara.
Em On the Psychology and Pathology of So-called Occult Phenomena, expôs pela
primeira vez os conceitos de "arquétipos" e "inconsciente
coletivo". Jung descobriu que determinados padrões geométricos e
simbólicos tendiam a recorrer espontaneamente nos desenhos, nas pinturas e nos
sonhos dos seus pacientes. Os conceitos antigos dos filósofos gnósticos e dos
cabalistas cristãos, especialmente o seu simbolismo, ocorrem espontaneamente
ao longo de todas as suas obras. Ele acreditava que esses padrões ocultos
fossem, por conseguinte, imagens espontâneas nas mentes das pessoas. Escritores
como o místico Jakob Boehme, que viveu no século XVII, expressaram-se
longamente sobre símbolos geométricos e alquímicos que, para Jung, eram
tão importantes para a idade moderna quanto os postes com letreiros para a
geografia da mente, exatamente como o eram no século de Boebme os símbolos do
Princípio Divino.
Essas idéias foram
retomadas por escritores como Maskell, que via no simbolismo das catedrais a
atuação insensata de autômatos ignorantes, levando à frente a sua tarefa de uma
maneira inconsciente. Jung mostrara que os padrões arquetípicos gerados
espontaneamente correspondiam com perfeição ao simbolismo tradicional da
geometria sagrada, de maneira que aquela interpretação era inevitável. O núcleo
da corrente ortodoxa da geometria sagrada fora relegado aos livros e às
revistas de corpos ocultistas e às teorias de indivíduos excêntricos como
Claude Bragdon e Antoni Gaudí.
Antoni Gaudí é uma
figura importante, se não enigmática, na arquitetura moderna. Católico romano
devoto, Gaudí considerava toda ação um ato de piedade, e não menos a sua
arquitetura. Mais por conveniência do que por fundamentação lógica, os
historiadores da arte categorizam suas obras únicas de fantasia canônica
no saco de gatos do Art Nouveau. Os escritores tenderam a enfatizar o bizarro ou
o aspecto inovador da sua obra em detrimento da tradição canônica dentro da
qual ele operava conscientemente. Embora sublinhem as inscrustações orgânicas -
os azulejos policromados, os bonecos de cacos de cerâmica, os ferros retorcidos
e as paisagens de pesadelo são um sistema de geometria sagrada cujas origens
podem ser remontadas ao ad triangulum medieval da Catedral de Milão e aos
esquemas proporcionais de Vitrúvio.
Diferentemente de
muitos outros expoentes da geometria sagrada moderna; Gaudí era totalmente
ortodoxo em suas crenças religiosas. Era católico romano, com uma devoção
especial ao culto da Virgem. Em cada um dos dias da sua longa vida, ele
assistiu aos serviços religiosos apropriados, nos últimos anos chegava a
caminhar muitas milhas para fazê-Io. Naturalmente, seu ponto forte era o desenho
de igrejas, embora também tivesse desenhado muitos blocos de apartamentos.
Acreditou-se que um deles, a Casa Mila, seria a base para uma vasta efígie da
Virgem. Essa singularidade, todavia, nunca foi completada, pois a construção coincidiu
com a sublevação anarquista de 1909, quando muitas fundações religiosas foram
alvo de ataques impiedosos dos insurrecionistas anticlericais. Após a repressão
sangrenta da sublevação, o patrono de Gaudí temeu uma outra revolução, talvez
mais bem sucedida, e resolveu não mais marcar sua propriedade com esse estilo.
A com una anarquista que se bateu contra a cidade durante o ano de 1936
realmente atacou igrejas, mas poupou a Casa Mila, de maneira que sua recusa se
mostrou realista.
A obra-prima de
Gaudí, cuja construção ainda está em andamento, foi o Templo Expiatório da
Sagrada Família (a Sagrada Família), Esse edifício enorme, que levará um outro
século para ser completado, foi concebido como um símbolo do renascimento
cristão da cidade de Barcelona. Gaudí trabalhou muitos anos no projeto, que
ainda era fragmentário por ocasião da sua morte em 1926. Seus planos e modelos
foram grandemente destruídos durante a Revolução Espanhola dos anos 1930, mas
seus seguidores reconstruíram-nos posteriormente a partir de material já
publicado. Pretendia-se que a Sagrada Família fosse a progressão lógica da
arquitetura gótica "libertada do flamboyant", com a utilização de
técnicas modernas para evitar a necessidade de expedientes estruturais tais
como os arcobotantes. De fato, o interesse de Gaudí pela geometria esotérica
fez dele um dos primeiros arquitetos dos tempos modernos a empregar o arco
parabólico e, por essa razão, seus edifícios contêm aquilo que à primeira vista
parece ser um conceito ridículo - pilares inclinados. Estes pilares, todavia,
são o resultado de se considerar a construção de um edifício como um todo que
integra mecânica e organ:camente todas as partes de maneira que ela ecoe
espiritualmente, se não funcionalmente, a natureza "abrangente" da
arquitetura gótica.
Diferentemente dos
edifícios "copiados", a Sagrada Familia enquadra-se verdadeiramente
na tradição da geometria sagrada porque utilizou esse sistema para determinar
as suas formas. Essas formas, verdadeiramente modernas para a época, devem
pouco ou nada aos estilos passados e, por causa da sua geometria subjacente,
são adequadas ao propósito para o qual foram planejadas. Este fato, e não a
forma externa, separa a arquitetura realmente sagrada da arquitetura meramente
inventada ou derivada.
Na mesma época em que
surgiram as maiores obras de Gaudí, as idéias do revivescimento dos rosacruzes
e as descobertas teosóficas de Madame Blavatsky estavam sendo sintetizadas
pelo gênio oculto de Rudolf Steiner num sistema novo, a Antroposofia. Nem magia
nem religião, a Antroposofia pretendia ocupar um novo nicho entre o artístico e
o místico. Steiner, fundador e mentor do credo, construiu uma sede que era uma
reprodução do espírito dos templos antigos em tudo menos no nome. Incorporando
uma geometria sagrada verdadeira, esse templo, conhecido como Goetheanum, era
a culminação de muitos anos de pesquisa. Em 1911, Steiner pronunciou uma
conferência intitulada The Temple is Man, em que discutiu os princípios que
subjazem aos templos da antigüidade. Todavia, diferiu do historicismo usual dos
seus contemporâneos, pois não falava só dos templos antigos, mas também dos do
futuro. Estes, entre os quais se incluía o seu Goetheanum (embora na época
fosse conhecido como Johannesbau), deveriam diferir dos templos antigos no fato
de serem emblemas do homem que recebera o espírito em sua alma.
Em 1914, em Dornach,
na Suíça, Steiner iniciou a construção do seu magnum opus, o projetado
Johannesbau. Na época, passara da Teosofia à nova Antroposofia e, por
conseguinte, os símbolos que pretendia utilizar eram considerados obsoletos.
Tendo extraído da teoria do mundo de Goethe a direção de sua nova arte
antroposófica, modificou o nome do templo para Goetheanum.
Steiner acreditava
que o Goetheanum era um desenvolvimento do desenho do templo que provinha da
antigüidade até sua época por linha direta. Suas idéias enquadravam-se
perfeitamente na tradição que esbocei nos primeiros capítulos - o templo como
um símbolo do corpo do homem. Para o Goetheanum, erigiu-se toda uma teoria
corrente da evolução espiritual simbólica da arquitetura. Desde os tempos
antigos, afirmou Steiner, até a época do Templo de Salomão, reinou o princípio
humano. Várias características de sua maneira de ser foram expressas no templo.
À época de Cristo, o arco e o domo simbolizavam a encarnação do vivo e a
excarnação do morto, e as catedrais góticas, baseadas no padrão da cruz,
simbolizavam o sepulcro de Cristo.
Steiner acreditava
que, no período medieval tardio, brotara um novo estilo de arquitetura que
pretendia abranger toda a humanidade e levá-la a um Cristo subido aos céus.
Todavia, esse edifício sobreviveu apenas na poesia, o perfeito Castelo do Graal.
Foi na direção desse símbolo ideal que Steiner trabalhou.
O Goetheanum,
construído, era uma estrutura de dois domos que os incorporava de uma maneira
sem precedentes. Como os templos pagãos antigos, estava orientado na direção
leste-oeste, com entrada pelo lado oriental. Um desenho engenhoso, baseado no
triângulo 3:4:5 pitagórico, serviu como base para esses dois domos que
simbolizavam não só a fusão dos princípios masculino e feminino, mas também a
estrutura do cérebro humano. É nessa analogia que a geometria é especialmente
engenhosa. No cérebro, a intersecção focal dos dois círculos que compõem a
geometria básica do templo, está o corpo pineal. Em termos ocultistas, esse
órgão é a sede da alma, o antigo terceiro olho de nossos antepassados arcaicos.
Steiner via a pineal em termos do Graal.
Steiner disse várias
vezes que as formas arredondadas, art nouveau, do Goetheanum foram exigidas
por uma modificação na função de um templo. Na antigüidade, o homem tinha de
encarnar e vir das Esferas Cósmicas à Terra, de maneira que o templo devia ser
construído de forma retangular para que o ego divino aí pudesse residir. Na
época moderna, todavia, o homem elevava-se do túmulo e se manifestava em sua
forma etérea. Por essa razão, a forma arredondada era a mais apropriada. E,
também porque simbolizava antes o mundo orgânico do que o terreno, o templo
foi feito de madeira, um material que se conforma à teoria goethiana da
metamorfose. Infelizmente, a insistência de Steiner na madeira tornou-o um
alvo ideal dos incendiadores que o queimaram no final de 1922.
Como uma catedral
antiga, o Goetheanum foi aborrotado de simbolismo esotérico. Janelas de vidro
colorido com motivos adequados expunham a função simbólica do templo. Na
entrada, a janela simbólica Ich shaue den Bau (Eu contemplo o edifício)
demonstrava que a elevação pretendia representar um homem em pé, apesar de o
templo pretender ser um homem. Este planejamento esotérico como parte de um
ethos consistente é típico de Steiner, o gênio místico. Quão atípico ele é em
relação ao espírito moderno!
Durante a carnificina
da Grande Guerra, os artistas dos países neutros, como a Suíça e os Países
Baixos, foram levados por aquele espetáculo atroz a rejeitar a arte de uma era
que gerara a lesão corporal dolosa da Frente Ocidental. Artistas desiludidos de
Zurique organizaram o movimento anárquico chamado Dada, que rejeitou todo o
conceito de arte e procurou deliberadamente infringir o convencional. Nos
Países Baixos, que possuíam uma longa tradição de arte "puritana",
desenvolveu-se o novo movimento em arte e arquitetura, conhecido como De
Stijl. Baseado em linhas retas desprovidas de adorno, o De Stijl foi visto como
uma rejeição dos anéis floreados do Art Nouveau, que os artistas acreditavam
ser decadente, e das fantasias multifacetadas do Wendingen, eu a Escola de
Arquitetura de Amsterdã, cujas estruturas espantosas ainda dominam partes de
Amsterdã sessenta anos depois.
O De Stijl foi
conscientemente baseado em princípios metafísicos e em proporções geométricas.
Alguns dos seus conceitos derivaram dos escritos de Spinoza (1632-1677),
filósofo místico judeu holandês. Spinoza acreditava que os objetos separados e
as almas individuais não estão totalmente separadas, mas são aspectos
integrais do Ser Divino. Ele escreveu que "toda determinação é uma
negação": que a definição das coisas só é possível se se disser o que elas
não são. Isto envolve definir as coisas por seus limites, os pontos em que elas
debçam de ser elas próprias e se tornam algo que não são. Da mesma maneira, nos
muitos escritos teóricos do De Stijl, a ênfase constante recai sobre as
relações entre as coisas: a geometria subjacente é mais importante do que o ser
físico.
O arquiteto Theo van
Doesburg e o pintor Piet Mondriaan, as luzes condutoras do De Stijl, acentuaram
constantemente que seu objetivo era a recriação da harmonia universal. Como
Spinoza, eles acreditavam qU6 todas as emoções rompiam esse equilíbrio. Daí se
terem esforçado, através da aplicação da geometria sem adornos, por transcender
as exigências temporárias do mundo. Spinoza afirmara que a saúde espiritual
repousa no amor de uma coisa imutável e eterna. Mondriaan escreveu: "O que
é imutável está acima de toda miséria e de toda felicidade: equilíbrio. Por
meio do imutável que existe em nós somos identificados a toda a existência; o
mutável destrói nosso equilíbrio, limita-nos e nos separa de tudo o que não é
nós".
Este não é um
sentimento comum entre os artistas modernos, pois tendemos a ver o pintor
moderno como um indivíduo centrado em si mesmo. Todavia, Piet Mondriaan estava
envolvido com o místico; membro da Sociedade Teosófica Holandesa, tirou uma
fotografia de Madame Blavatsky em seu estúdio. Artistas teosóficos estavam
tentando criar uma nova ordem baseada na sabedoria antiga, mas num estilo
totalmente moderno. Artistas como o pintor moderno Wassily Kandinsky e os
compositores Scriabin e Stravinsky, todos eles inovadores extraordinários,
também eram adeptos da crença teosófica.
Além dessas
influências místicas de Spinoza e Blavatsky, havia também o efeito do místico
alemão contemporâneo Dr. Schoenmaekers. Em 1916, quando a idéia do De Stijl
esfava sendo discutida, Schoenmaekers vivia em Laren, a mesma cidade em que
moravam Mondriaan e Bart van der Leck. Em 1915, foi publicado o influente livro
The New Image of the World, de Schoenmaekers, seguido de The PrincipIes of
Plastic Mathematics no ano seguinte. Sua abordagem mística da geometria
influenciou enormemente as idéias do novo movimento. Schoenmaekers escreveu:
"Queremos penetrar a natureza de maneira que a construção interior da
realidade nos seja revelada". Baseado nesses conceitos místicos, um
estilo aparentemente materialista e totalmente moderno é na verdade sublinhado
por um ethos antigo, emergindo com a corrente do pensamento ocultista que
subjaz à forma arquitetônica.
A sensação geral nos
anos 1920 era a de que uma nova era que estava começando manifestava-se de
diversas maneiras. Na Alemanha, levou à ascensão de HitIer e à nova ordem do
Nacional-socialismo. Na Rússia, os bolchevistas tentaram reestruturar a vida à
imagem da filosofia marxista. Artistas rejeitaram o velho academicismo e
voltaram, como a escola De Stijl, àquilo que consideravam formas geométricas
puras, essenciais, desprovidas de ornamentos. Entre a proliferação de novos
credos, a geometria sagrada platônica antiga ganhou novamente a
superfície. Um dos maiores ourives do século XX, Jean Puiforcat, criou obras
verdadeiramente clássicas cujas formas se baseavam nos sistemas canônicos
antigos de geometria e de proporção. Numa carta enviada ao Comte Fleury,
escrita em 1933, Puiforcat explicou como descobrira o sistema que utilizava em
suas xícaras e em seus vasos art deco:
"Mergulhei na
matemática e bebi em Platão. O caminho estava aberto. Dele, aprendi os meios
aritméticos, harmônicos e geométricos, os cinco famosos corpos platônicos
ilustrados por Leonardo: o dodecaedro, o tetraedro (fogo), o octaedro (ar), o
icosaedro (água) e o cubo (terra).”
Os desenhos de
Puiforcat, muitos dos quais ainda sobrevivem, trazem como legenda a expressão
"Tracé harmonique, figure de départ R V2" e demonstram o mesmo
esforço pela harmonia universal eterna que encontramos em todos os períodos de
empenho artístico.
No mesmo veio de
universalidade, o sistema proporcional elaborado pelo arquiteto moderno Le
Corbusier surgiu muitos anos depois. Por volta de 1950, num período de
relativo otimismo e na crença de que o governo do inundo já passara o seu momento
crítico, Le Corbusier considerou ser terrível o fato de que a metrologia do
mundo estivesse dividida em dois campos opostos. As nações anglo-falantes ainda
aderiam ao sistema imperial inglês de medição, ao passo que o resto do mundo
desenvolvido adotara, oficialmente pelo menos, o sistema métrico. Le Corbusier
entendia que a proporção era a consideração fundamental dos arquitetos e dos
construtores e que a medida era um instrumento para facilitar a construção.
Diante de uma prática de edificação que operava ambos os sistemas na França e
na América do Norte, voltou-se contra os problemas quase insuperáveis de
trabalhar com dois sistemas incomensuráveis de medição.
Para ultrapassar esta
dificuldade, e para estabelecer um meio de criar proporções harmônicas, Le
Corbusier voltou ao cânone grego antigo da Seção Dourada. A partir dele, por
muitos experimentos geométricos complexos, chegou a um sistema modular
proporcional coerente a que chamou Modulor - o módulo da Seção Dourada. Como a
geometria de Puiforcat, a de Le Corbusier derivou de Platão e dos geômetras
gregos, uma geometria que poderia ter sido atribuída a Alberti ou a Wren. O
Modular foi concebido como um instrumento de mediçãG. Como a geometria sagrada
antiga, ele se baseava con juntamente na matemática abstrata e nas
proporções inerentes à estrutura humana.
Um homem com o braço
levantado fornece os pontos determinantes da sua ocupação do espaço: o pé, o
plexo solar, a cabeça e as pontas dos dedos do braço levantado produzem três
intervalos. Esses pontos estão numa Série Fibonacci, uma série de razões da
Seção Dourada. Dessa "medida natural" deriva um complexo de
subdivisões que constituem a essência do Modular. Mas, mesmo com um sistema
baseado unicamente em razões, é preciso alguma medida inicial.
Originalmente, Le
Corbusier fez de seu ponto de partida um homem hipotético de 1,75 metro de
altura - a "altura francesa", como afirmou depois. Os módulos
desenvolvidos a partir dessa unidade provaram, infelizmente, ser de difícil
manuseio e incomensuráveis com a vida cotidiana. Então Le Corbusier decidiu
procurar um ponto de partida melhor. Seu colaborador Py observou que, nos
romances policiais ingleses, os hérois, como os policiais, possuem invariavelmente
seis pés de altura. Partindo dessa "altura inglesa" de seis pés,
transferiu-a para o sistema métrico: 182,88 centímetros e um novo
Modulor foi desenhado. Para sua satisfação e surpresa, as divisões desse novo
Modulor baseado na medida inglesa transferiram-se para figutas redondas de pés
e polegadas - algo não surpreendente para um sistema natural de medida.
Le Corbusier afirmou
repetidas vezes que seu Modulor derivado da medida de seis pés fora baseado na
escala humana, da mesma maneira como os geômetras provaram, especialmente na
Renascença, que o corpo humano está proporcionalizado de acordo com a regra
dourada. Essa abordagem quase-mística surge em toda a obra de Le Corbusier.
Embora ele tenha sido educado e criado nos termos do materialismo do começo do
século XX, ecos do primitivo ethos do homem como o microcosmo podem ser
percebidos aqui e ali. A sua afirmação de que a arquitetura deve ser um
algo do corpo, um algo da substância bem como do espírito e do cérebro,
incorpora perfeitamente a fusão do físico, do espiritual e do intelectual que
tem sido característica da melhor arquitetura fundada na geometria sagrada.
Le Corbusier falou
repetidas vezes sobre "flanar diante da Porta dos Milagres" e, para
abrir caminho através dessa porta, voltou à Seção Dourada. Todo e qualquer
objeto de seu escritório estava eventualmente posicionado segundo o Modulor, um
sistema rígido e inflexível, ligado a uma forma inconsciente de geomancia. Mas,
embora fosse baseado em sólidos princípios antigos, a utilização rígida do
Modulor para seja o que for é apenas parte integrante dos métodos disponíveis.
Com a tecnologia do mundo moderno, usa-se apenas o hemisfério intelectual do
cérebro, rejeitando-se o hemisfério intuitivo. Os geomantes e os geômetras de
outrora sempre temperaram seus modelos geométricos com a intuição pragmática,
mas a tendência moderna em todas as coisas consiste no extremismo, forçando um
sistema à exclusão de todos os outros.
14. Ciência:
O Verificador da Geometria Sagrada
A descoberta e a
aplicação da eletricidade por Faraday, Edison, Siemens e Tesla durante o século
XIX estabeleceram os fundamentos da era moderna. As cidades puderam crescer com
o transporte público barato oferecido pelo ônibus elétrico e a eletricidade forneceu
energia para tudo, desde os trens subterrâneos até a iluminação e as
telecomunicações. Os pioneiros dessa nova energia consideravam-na sujeita a
várias leis imprevistas. Os ocuItjstas, fascinados pela nova energia, começaram
a ver no seu circuito e nas suas expressões físicas um paralelo dos seus
poderes.
O "poder",
na forma de uma energia canalizável análoga à eletricidade, tem sido estudado
tanto por mágicos como por romancistas. Exemplificada como o fictício vril do
romance The Coming Race de Bulwer Lytton, a existência de um poder similar tem
sido encontrada por antropólogos em várias partes do mundo. O misterioso mana
dos Mares do Sul, que se diz ter erguido as várias estátuas de pedra da Ilha de
Páscoa, foi comparado às energias ióguicas dos homens santos asiáticos. Entre
os escritores influentes, Madame BIavatsky e James Churchward discutiram as
possibilidades dessas energias.
Os experimentos
científicos do físico Chladni e de outros apontaram o caminho para a relação
entre a energia e os padrões geométricos. Chladni descobriu que uma película
delgada de areia espalhada sobre uma lâmina que vibra mecanicamente formaria determinados
padrões geométricos fixos que estariam relacionados ao comprimento de onda da
vibração. Pesquisas recentes sobre mistérios antigos sugeriram que os
possíveis comprimentos de onda de forças telúricas podem determinar as
geometrias de edifícios. sagrados. Considerando-se as noções antigas sobre a
harmonia, das esferas, talvez isto seja a fundamental geometria do
comprimento de onda do universo criado. Padrões de poder que agora estão sendo
examinados por detectores em várias partes do mundo e por Paul Devereux e sua
equipe do Projeto Dragão em Rollright Stones podem enquadrar-se nessa
categoria. Aqueles que detectam energia nas linhas ley acreditam que essa
energia pode ser parte de uma grade global que tem uma forma geométrica
precisa. Algumas pessoas Ijgam esses padrões até mesmo ao aparecimento de OVNI’s,
dos fantasmas, à perturbação psíquica e à ocorrência de combustão espontânea em
seres humanos.
A invenção do
microscópio no século XVII e seu aperfeiçoamento no século XIX levaram à
criação de todo um tema científico, o estudo das estruturas microscópicas. Com
a descoberta de que os animais, e as plantas em particular, são compostos de
células regularmente estruturadas, surgiu um interesse renovado pela
geometria. Cientistas tentaram criar uma base teórica para as estruturas geométricas
que estavam observando. Grandes cientistas como Lord Kelvin dedicaram-se a
estudar o acondicionamento geométrico das células e chegaram às velhas formas
de Arquimedes e de Platão. A obra de F. T. Lewis mostrou que a estrutura
celular de vários vegetais tende para o corpo de 14-hedron (tetrakaidekahedron)
de Arquimedes.
D'Arcy Thompson, que
combinou um conhecimento enciclopédico de escritos clássimos com uma abordagem
extremamente perceptiva da biologia, talvez tenha feito a maior contribuição à
nossa compreensão da harmonia divina. Na sua obra seminal On Growth and Form,
publicada no crucial ano de 1917 (o ano da Revolução Russa, da Teoria da
Relatividade de Einstein e do surgimento do De Stijl) Thómpson delineou as
relações íntimas entre a morfologia das estruturas orgânicas e as forças
físicas que moldam o cosmos.
Thompson afirmou que
a estrutura básica é em última instância a mesma tanto no ser vivo quanto no
não-vivo e que, assim, pode ser determinada por uma análise física do sistema
material das forças mecânicas. Ela representa uma harmonia e uma perfeição intrínsecas,
algo exibido por um instrumento musical afinado, obra de verdadeiro artista e
de tudo que está "junto" na natureza. A ciência ortodoxa, no
presente, afirma que as formas estruturais dos organismos vivos são totalmente
controlados por um padrão genético inato impresso no núcleo de cada célula.
Thompson acreditava que as formas de vários órgãos e organismos foram moldadas
pelas forças físicas que agem sobre elas. Descobriu que a forma dessas estruturas
ecoa exatamente a forma da força física. As formas em miríade da estrutura
orgânica existem em conformidade com as leis que governam todas as coisas. Sua
beleza incrível origina-se no equilíbrio que é intrínseco à sua forma
"natural", sua conformidade com as leis geométricas inatas do
universo, A concha do Nautilus PeroIado é formada de acordo com a espiral
equiangular, como o são os chifres de determinados carneiros. Outras formas
geométricas clássicas ocorrem em toda a natureza.
A metafísica orgânica
de Thompson nunca foi muito bem vista pelos cientistas ortodoxos. Suas idéias
evolutivas estavam e estão fora de moda e sua abordagem holística opõe-se às
tendências reducionistas da ciência moderna. Por outro lado, sua abordagem científica
tornou suas idéias aparentemente inacessíveis àqueles que se interessam pelo
lado esotérico da vida. Assim, sua obra continua sendo pouco lida naquelas
áreas onde ela poderia despertar esclarecimentos adicionais. As idéias de
Thompson, enquanto desprezadas pela ciência estabeleci da, não podem ser
refutadas. Talvez sejam afirmações como a seguinte que o coloquem para fora do
âmbito da ciência materialista e para dentro da corrente do pensamento ocultista
ocidental:
"Eu sei que, no
estudo das coisas materiais, o número, a ordem e a posição são o indício triplo
do conhecimento exato; que esses três; nas mãos dos matemáticos, forneceram o
'primeiro esboço para um croqui do universo' (...) Pois a harmonia do mundo é
manifestada em forma e em número e o coração e a alma e toda a poesia da
Filosofia Natural estão embebidos do conceito da beleza matemática.”
Vinte anos após o
aparecimento do livro de Thompson, os técnicos em eletrônica da Alemanha
nazista aperfeiçoaram um instrumento que deveria revolucionar nosso
conhecimento sobre o mundo microscópico interior da natureza - o microscópio
eletrônico. Esse novo instrumento, que utiliza antes os elétrons do que a luz
visível, capacitou os cientistas a ver estruturas milhares de vezes menores do
que aquelas que eram visíveis com microscópios de luz. Não foi antes dos anos
50 que as técnicas de preparação de espécimens tornaram possível aos biólogos
estudar a estrutura dos organismos vivos com qualquer medida de êxito. Todavia,
quando muitos vegetais e animais unicelulares foram examinados, verificou-se
que eles formavam estruturas inesperadas (conhecidas como "escalas")
cujo arranjo e forma aderiam estreitamente aos esquemas antjgos da geo metria
sagrada. Sendo estruturas orgânicas produzidas de acordo com as leis enumeradas
por Thompson em On Growth and Form, elas demonstram novamente, de maneira
convincente, a harmonia divina. Os organismos marinhos que o autor estudou
pessoalmente com o microscópio eletrônico demonstram os princípios do ad trian gulum
e do ad quadratum desenvolvidos pelos mestres maçônicos da época gótica. Eles
são, de fato, reflexos da ordem natural do universo.
As idéias dos antigos
sobre a ordem universal como um aspecto do criador estão sendo verificadas
pela ciência. Elas não podem mais ser descartadas como fantasias de néscios.
No respeitado jornal científico Nature de 12 de abril de 1979 apareceu um
artigo de B. J. Carr e M. J. Rees. Intitulado The Anthropic Principie and the
Structure of the Physical World, abrangeu de maneira altamente técnica e
matemática as "constantes" microfísicas que governam as
características básicas das galáxias, das estrelas, dos planetas e do mundo
cotidiano. Os autores apontaram "muitas relações divertidas entre as
diferentes escalas" do universo. Por exemplo, o tamanho de um planeta
é a média geométrica dos tamanhos do universo e do átomo e a massa de um homem
é a média geométrica entre a massa de um planeta e a massa de um próton. Outras
variáveis bastante criticáveis estão delicadamente equilibradas na estrutura
universal para possibilitarem a existência da vida. Nos termos da ciência
materialista, essas recorrências notáveis são "coincidências" justas,
mas em termos metafísicos elas são exigência fundamental do criador. As médias
geométricas representadas pelo planeta e pelo homem ecoam a antiga visão de
mundo do microcosmo e do macrocosmo. A única diferença é a terminologia
moderna, não-metafísica. Não é de todo surpreendente para aqueles que estão
conscientes dos ensinamentos antigos o fato de que a pesquisa cosmológica
moderna poderia verificar o conhecimento hermético dos antigos.
As descobertas modernas
da ciência repousam naturalmente em termos materialistas. Todavia, toda ciência
é teoria e, como tal, está aberta a alterações radicais de interpretação à
medida que uma nova prova surja da observação e do experimento. A interpretação
que Everett fez dos muitos mundos a respeito da mecânica quântica postulada em
1957 afirma que em cada observação o universo ramifica-se num grande número de
universos paralelos, correspondendo cada um deles a um possível resultado de
uma observação. Nessa estrutura - que fof descrita pelo dramaturgo anárquico e
escritor Alfred Jarry, em seu romance neocientífico Exploits and Opinions of
Doctor Faustroll, Pataphysician e em Caesar Antichrist -, em que o observador
torna-se a personagem mais importante do jogo do universo, encaixa-se a figura
antropocêntrica que compreende todo o mecanismo universal - a figura do homem
microcósmico. Em Caesar Antichrist, Jarry resumiu a questão: "Posso ver
todos os mundos possíveis quando olho para apenas um deles. Deus - ou eu mesmo
- criou todos os mundos possíveis, eles coexistem, mas os homens dificilmente
podem vislumbrar um deles". Isto foi escrito meio século antes da idéia
de muitos mundos de Everett.
J. A. Wheeler, no
livro Gravitation, publicado em 1971, afirmou esse conceito poético-filosófico
numa forma matemática científica. Ele considerou um conjunto infinito de
universos, cada um com leis físicas constantes e variáveis. A maioria desses
universos poderia ser natimorta, incapaz de, por força de sua física e de sua
geometria peculiares, permitir que qualquer ação interessante ocorra em seu
interior. Apenas aqueles que se iniciam com as leis devidas e as constantes
físicas podem desenvolver-se para um estágio em que possam tomar consciência de
si mesmos. Assim, nosso universo existente, capaz de sustentar o nível
material de existência, é por sua própria natureza um caso especial, com uma
física apropriada e, por conseguinte, uma geometria para a existência. Essa
geometria subjacente, reconhecida desde a aurora da humanidade como álgo especial,
é de fato um arquétipo da natureza única dessa fase da criação que possibilita
a existência do mundo material. Cada vez que se produz uma forma geométrica,
faz-se uma expressão da unicidade universal; ela é ao mesmo tempo única em
tempo e em espaço e também eterna e transcendente, representando o particular
e o universal.






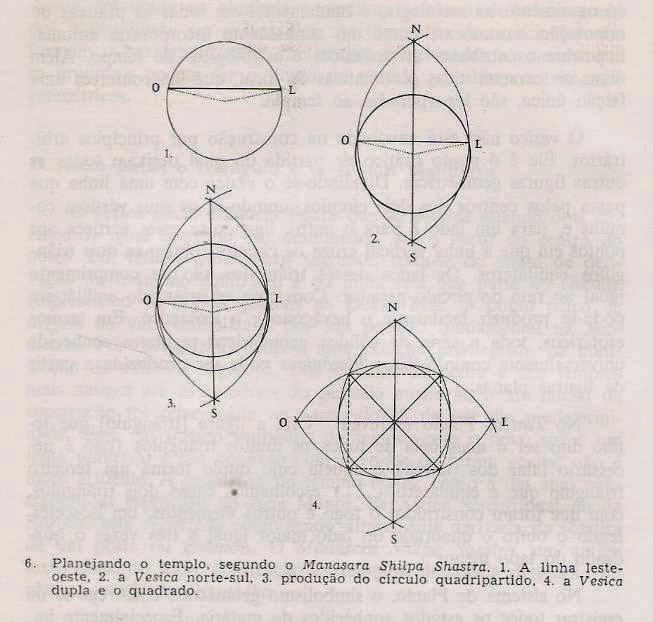






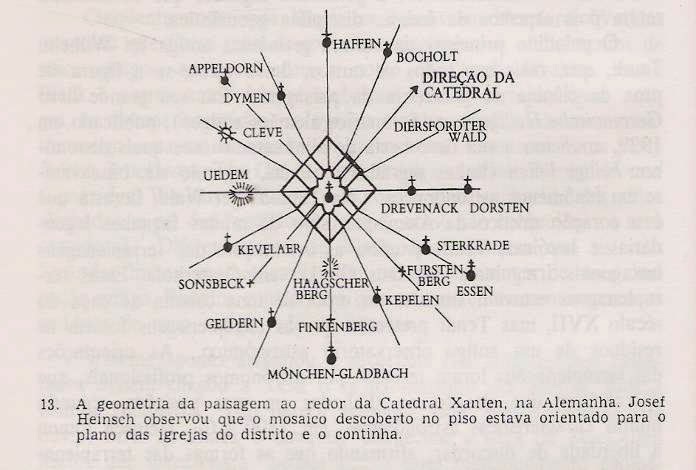



























Nenhum comentário:
Postar um comentário